1.はじめに
高分子材料は、空間スケールで言えばnmからμmまでのマルチスケール特性を有しているため、現象や物性の発現がどのスケールに起因するか注意して考える必要がある。実験・計測技術の発展に支えられて多くのメカニズムが明らかにされてきているが、それだけでは捉えきれない部分に関して、シミュレーション技術が重要な役割を果たしている。また、最近ではデータサイエンスを用いた物性予測なども進んできているが、シミュレーション技術はそこでも相補的な役割を担っている。
以下では、高分子のシミュレーション技術について代表的ないくつかの手法の概要、それぞれの連携、ソフトウェアなどを紹介する。各手法がターゲットとする空間スケールに注目して見ていくとわかりやすいため、小さなスケールから順番に説明する。なお、各手法の文献を挙げていくときりがないため、基本的には参考文献[1]を参照頂きたい。
2.量子化学・密度汎関数理論
主に数nm以下をターゲットとする手法で、分子や結晶内の電子状態をSchrodinger方程式に基づいて計算する。特に励起や分極、分子間力、化学反応など、物質の電子的な性質を評価する際に用いられる。分子軌道法(Molecular Orbital method : MO)や、電子密度を計算対象とすることで計算負荷が低減できる密度汎関数理論(Density Functional Theory : DFT)があるが、電子相関の取り入れ方や、基底関数の選び方などによって手法が細分化される[2]。
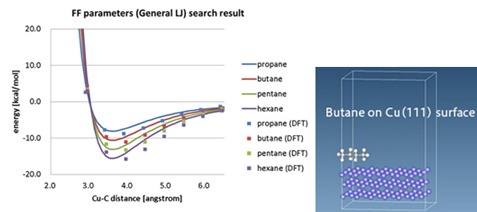
(左:propane/butane/pentane/hexane分子の吸着エネルギー曲線、右:計算モデル)
図1はCuの結晶表面に分子が吸着した際の、表面からの距離とエネルギーの関係をvan der Waals力を考慮したDFTで計算した結果(分子種ごとに点で表示)を示しており、後述の分子動力学で用いるためのLennard-Jones(LJ)ポテンシャルにフィッティングした曲線も併せて表示している。このような表面吸着エネルギーは界面の設計において重要となるが、妥当なLJポテンシャルパラメータが存在しないケースもあり、DFTなどによる評価が必要となる。
3.全原子分子動力学
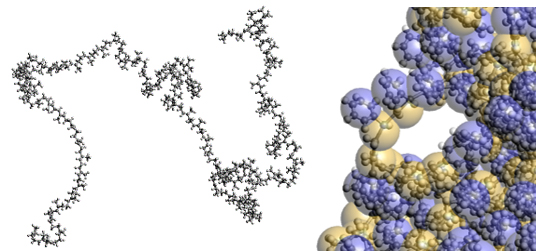
全原子分子動力学(Full Atomistic Molecular Dynamics : FAMD)は、一つの粒子(質点)が一つの原子を表し(図2左)、各質点のダイナミクスをNewtonの運動方程式に基づき計算する。各原子に働く力は関数とパラメータによって与えられ、その中には前述のLJポテンシャルなどが含まれる。パラメータはデータベースとして公開されていることが多いが、より精度を上げるため、前述のDFTのような一つ下のスケールの手法と組み合わせる。FAMDを用いることで、官能基など分子構造を変更した際の分子形状やダイナミクスへの影響を評価することができる。例えばバルク状態の高分子の密度や弾性率、自由体積の分布やその中の気体分子の拡散、配向(結晶)構造などが挙げられる。様々な用途に適用できるため普及しているが、一般的なコンピュータを用いる限り扱える空間スケールが10nm程度、時間スケールは最近のソフトウェアとハードウェア(GPUなど)を用いる場合でも100nsのオーダーであるため、例えば高分子の長時間の緩和現象を扱うには不足する。
4.粗視化分子動力学
粗視化分子動力学(Coarse Grained Molecular Dynamics : CGMD)では、一つの粒子(質点)がいくつかの原子の集まりを表現する(図2右)。これによって、FAMDと比べて時間空間ともに大きなスケールの現象を扱うことが可能となる(10~100nm、μsなど)例えばゴム材料の引っ張り特性を評価するのであれば、ゴム領域を扱えるような時間(変形速度)の計算が必要となるが、FAMDでは難しくCGMDを用いることで可能となる。粗視化ユニット間の相互作用(粗視化ポテンシャル)はFAMDをベースに決定する場合[3]と、簡易的なパラメータを与えて計算後に意味づけをする場合がある。
図3ではStyrene-Isoprene-Styrene(SIS)のようなトリブロック共重合体が形成する相分離構造(熱可塑性エラストマー)の一軸伸長時の挙動を評価している[4]。初期構造の構築には後述の平均場法の計算結果を用いている。伸長時のドメインや分子鎖の変形の様子が捉えられている。
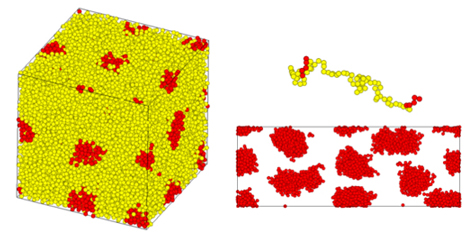
(左:初期構造、右:変形中の構造(上側は一本の鎖、下側はドメイン構造))
5.散逸粒子動力学と平均場法
散逸粒子動力学(Dissipative Particle Dynamics:DPD)[5]はCGMDの一種であるが、粒子間相互作用にすり抜けを許すソフトポテンシャルが用いられることで、相分離やフィラー分散構造の評価などに適している。ダイナミクスには流体効果も含まれている。平均場法(Mean Field : MF)では、高分子の各成分を濃度(体積分率)場で表現することで相分離のダイナミクスや平衡状態までを評価する。各成分の拡散および流体力学とのカップリングが可能である。中でも自己無撞着場理論(Self-Consistent Field Theory : SCFT)を用いることで高分子鎖の形状も考慮できる。これらの手法では成分(粒子)間の相互作用としてFlory-Hugginsのχパラメータが用いられるが、前述のFAMDや、量子化学計算を用いて推算する手法[6]も提案されている。
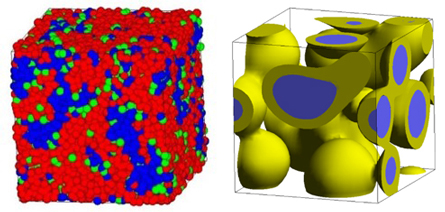
図4(左)はDPDを用いて計算した高分子電解質と水の相分離構造、図4(右)は平均場法を用いて計算した高分子3成分系の相分離(コア・シェル)構造である。数100nmまでの空間スケールがターゲットとなる。
6.レプテーションダイナミクス
高分子鎖を絡み合い点間分子量の単位で粗視化することで、高分子鎖の絡み合い構造に基づくレプテーション(reptation)ダイナミクスを計算することができる。Slip LinkモデルやPrimitive Chain Network(PCN)モデル、前述のDPDに高分子鎖の絡み合い効果を加えることが可能なSlip Springモデル[7]などがある。
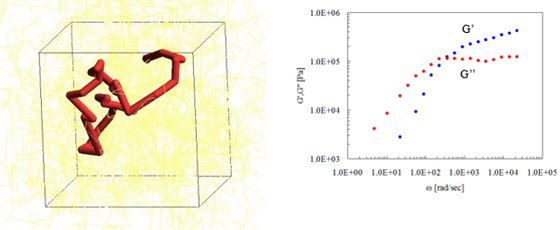
図5は、Polyisoprene(分子量約48,800)のG’(貯蔵弾性率)とG”(損失弾性率)を評価したものである。スナップショット中の折れ曲がりが絡み合い点に相当する。
7.連続体モデル
前述のDPDや平均場法で得られた相分子構造を用いて、連続体モデルに基づいた有限要素法(Finite Element Method : FEM)の計算を実施することで、平均弾性率や熱伝導率などの物性評価が可能となる。各成分の材料物性はパラメータとして入力される。図6(左)は図4(右)で得られた相分離構造に対して変形を加えた際の界面のひずみエネルギー分布を示しており、図6(右)はDPDで得られた高分子中のナノフィラーの分散構造に対して熱伝導計算を実施した際の熱流束の分布である。図6の計算では何かしらのシミュレーションで得られた構造を元にしているが、その代わりに散乱試験やCTなどのデータを用いることや、仮想的な構造を作り出すことで物性と構造の関係を数値実験するような活用法もある。
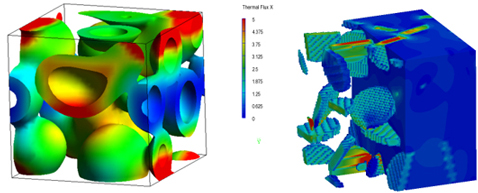
(左:相分離構造中のひずみエネルギー分布、右:ナノフィラー分散構造中の熱流束分布)
8.J-OCTAに含まれるエンジン(ソルバー)
量子化学・密度汎関数理論についてはSIESTAとABINIT-MPが同梱されており、Gaussianなどとのインターフェイスが提供されている。全原子・粗視化分子動力学についてはCOGNACとVSOP、GENESISが同梱されており、LAMMPS、GROMACS、HOOMD-blueとのインターフェイスが提供されている。散逸粒子動力学(DPD)については分子動力学と同様であるがGENESISとGROMACSには含まれない。平均場法についてはSUSHIが同梱されている。レプテーションダイナミクスについてはCOGNACおよびVSOPのSlip-Springモデルを適用したDPD機能、PASTA、NAPLESが該当する。連続体モデルについてはMUFFINが該当するが、その他商用ソフトウェアとのインターフェイスも提供されている。
- 高分子材料シミュレーション-OCTA活用事例集- 増補版”, 化学工業日報社 (2017)
- R.M.Martin, “物質の電子状態”, 丸善 (2010)
- C.Peter and K.Kremer, Soft Matter, 5, 4357 (2009)
- T.Aoyagi and T.Honda, J.Chem.Phys., 117, 8153 (2002)
- R.D.Groot and P.B.Warren, J.Chem.Phys., 107, 4423 (1997)
- K.Okuwaki, Y.Mochizuki, H.Doi, and T.Ozawa, J.Phys.Chem.B, 122, 338 (2018)
- Y.Masubuchi, M.Langeloth, M.C.Bohm, T.Inoue, and F.Muller-Plathe, Macromolecules, 49, 9186 (2016)
- ※ 記載されている製品およびサービスの名称は、それぞれの所有者の商標または登録商標です。
この記事の関連情報
技術ブログカテゴリ
新着記事
- 塗膜乾燥のシミュレーション — 塗布・塗装・電極プロセスの1D/3D解析入門
- マテリアルズ・インフォマティクス(MI)とは?
AI×シミュレーションで加速する次世代材料開発 - リアルワールドの自動車衝突安全に向けて(2)~ISOレーティング~
- 分子シミュレーションで設計するプラスチックリサイクル
- 形状設計フェーズでの組み立て精度向上によるコスト削減
~ 組み立てCE検討ツールのご紹介 ~ - JSOLが考える「溶接シミュレーションと工場デジタルツインが実現する工程設計」について講演しました
- リアルワールドの自動車衝突安全に向けて
- 機械学習で加速する材料シミュレーション技術
- ノウハウ不要!樹脂の複雑な材料特性を簡単にフィッティング 〜 材料同定ツールと高精度ユーザーサブルーチンの活用事例 〜
- 樹脂材やゴム材の高精度予測に向けたパラメータ同定
