金属だって記憶できるんだぞ - 形状記憶合金（SMA）その２ -

アメリカ人となじむには映画「カサブランカ」のセリフぐらい言えないといけない、と述べた（本コラム2008年度Vol.11）。

Where were you last night?
That's so long ago. I don't remember.
Will I see you tonight?
I never plan that far ahead.^[1]
これをボギー（ハンフリー・ボガード）でなく宇崎竜童さん風に言うなら

「きのうどこにいたの」
「そんな昔は憶えちゃいねー」
「今晩つきあってよ」
「そんな先のことは、ちとわかんねーなー」

といったところか。
ところで
形状記憶合金（Shape Memory Alloy, 以下では略してSMA）なら、きちんと憶えている。

あれは一方向メモリのSMAの解析が一段落した１９８６年頃のことだった。
N助教授がにこにこして「ちゃーんと教育したらSMAに二つの形状を記憶させられるぞ」
見せてくれたのがSMAのパイプの図１のようなものであった。縦軸がパイプの外径Doであり、横軸が温度 ℃ を表している。

まず左図の「点線」のヒステリシスを説明する。出発点は上側左端だ。－20℃から徐々に温度をあげると、しばらく外径Doは変化せずにフラットのまま右に進む。温度As（35℃付近）からカーブは下降を始め（つまり外径Doの収縮が始まり）温度Af（55℃付近）でほぼ収縮は終わりに近づき75℃ぐらいでほぼ落ち着く。逆に、そこから温度を下げていくと同じ経路を辿らず、ずっと下側を左向きにフラットに通り、温度Ms（13℃付近）から膨張がはじまり温度Mf（-10℃付近）でほぼ終わる。これが図１の左側の図のヒステリシスの説明である。
収縮過程の途中で（42℃ または、45.5℃で）クーリングを始めた場合が実線で描かれている。右側の図はクーリングの途中で加熱をはじめた場合である。相変態のはじまる温度As,やMsなどのAやMの記号はオーステナイト、マルテンサイトの結晶構造にちなんでいる。この場合のSMAはニッケルとチタンの合金であり、As、Af、Ms、Mfなどは事前の教育処理を通じて決まる（これらの詳細は文献^[2]に詳しいが入手はかなり難しい）。

以降の本コラムの内容は主として^[3]にしたがっている。

ところで、図１を大げさに言えば、半導体や青色ダイオードなみの？応用分野がちらつく。たとえば鋼管継手用のカップラーとして用いれば「温度の調整でカップラーを閉じたり開いたりできる」^[4]。沸騰したお湯に漬けるとはずれる繋ぎ目など面白いではないか^[5]。

しかし、ことは簡単におさまらない。
図１はフリーの状態でのパイプの収縮と膨張であった。しかし、カップラーとして用いる場合は相手あっての話だ。そこで繋がれるパイプを単純化したものを内管として差込み、温度を上げることにより内管の周方向に生じる応力をstrain gaugeで測定したのが図２である。SMAカップラーの初期の内径は53ｍｍ、肉厚は３ｍｍである。

図２では内管の外径を４種類変えた場合のヒステリシスが描かれている。とりあえず一番上側まで達しているヒステリシスを簡単に説明する。外径52ｍｍの内管（SUS）が挿入された場合（したがって内径53ｍｍのSMAカプラーとの平均隙間は0.5ｍｍ）を温度0℃から徐々に上げていく。その間に35℃付近でAsを通過するので収縮を開始するが内管とすぐには接触しないので圧縮応力は生じていない。40℃位から接触がはじまり締め付けにより圧縮応力は上昇しはじめる。100℃で圧縮応力は約70MPa程度まで達する。次に、温度を下げると同じ道を辿らず、上側を通ってやや緩慢に内管の圧縮応力は下降し（つまりSMAカップラーは膨張して締め付け力を弱め）10℃付近で両者は離間して圧縮応力は0に戻る。
内管の外径を細くした場合、それだけ初期のクリアランスが大きくなり接触のはじまるタイミングが遅くなる。その数ミリの差が100℃での圧縮応力に敏感に影響していることがわかる。そして注目すべきは「温度Af（55℃付近）を過ぎても圧縮応力が上がりつづけている」ことである。
図１のAsやAfはどうなってしまったのであろうか？
さて、このやっかいなカップラーの解析用の「モデル化」を考えてみよう。当時、FORTRANのソースコードが公表されていたNIKE2Dをベースにする^[6]。そこでは温度ひずみは次式で与えられていた。

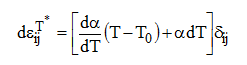
ここでは温度ひずみの増分、T は温度、α は非線形温度膨張係数、δ はクロネッカー記号である。これにならって次の式を大胆に想定しよう。

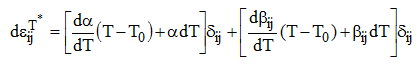
温度の変化にともなうSMAの相変態を一種の温度膨張（または収縮）に似かよったものだ、とわりきり、右辺に第２項を付け加えたものである。ここで β_ij は形状記憶効果による非線形の形状記憶係数（筆者が勝ってそう呼んでいる）である。この β_ij さえ決まれば後はこちらのもの。次の構成則（3）式に（2）式を用いればよいわけである。

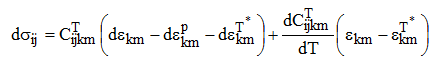
ここで は構成行列であり、 は塑性ひずみ増分である。 については文献^[6]に具体例が掲載されている。
問題となってくるのは（2）式での β_ij をどのようにして決めるかということになる。仮に β₁₁ を主メモリー軸方向としよう。相変態の間に体積変化がないとすれば β₂₂ ＝ β₃₃ ＝ －0.5 β₁₁ としてよいであろう。それ以外は（クロネッカ記号によりはねられるので）０とする。そこで焦点を β₁₁ だけに絞ろう。添え字11はなくてもよいが履歴ループでの位置を表す記号をつけることにしよう。