■橘サイバー研究所
Vol.33

スナップスルー(Snap-Through)と非線形計画法(nonlinear programming)
－話せば長いことながら入り口だけでも－

2014.07.02
この記事をシェア
著者プロフィール
橘 英三郎
  • 大阪大学名誉教授 建築工学

このような挙動をSnap-Throughなどと呼ばれたりする。では、この解析結果はどうして得たのか。ここで、例の学生の登場となる。

「単位ギリギリの絶妙？のバランスをねらう」

この問題の場合、「全歪エネルギーを最小にするときのX(1), X(2), X(3)を求める」

「多変数関数を最小化する手法」はオペレーションズ・リサーチ（Operations ResearchもしくはOR）の分野で発達しているので、そのワザを借りることにした。
具体的には非線形計画法における準ニュートン法を用いた。

その手順は以下となる。

X(1), X(2), X(3)からなるベクトルを｛ｘ｝とし、その変数で表された全歪エネルギーを S｛ｘ｝とする。
Δを与える。（方針：このΔに対する反力を求める。Δを色々変えて反力を求め図２が得られる）
ｋ＝１とする。（ｋは繰り返しのステップを表す）
変数と同じかずの行と列よりなる正方の単位行列を[Hk]の初期値とする。
適当に｛Xk｝を仮定する。おっと、この「適当に」は意外と初心者にはくせもの。
色々あるが、とりあえず、全て０としよう。

10 CONTINUE

次式より｛D} を求める。

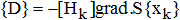
ここでgrad.(グラデュエント)の記号がでてくる。
びびることはない。差分近似で簡単に計算できる[3]。
[Hk] はこの一連の手順でヘシアンの近似逆行列の役割を果たしBFGS公式の主役となる。
次に、次式の値を最小にするαをきめる。（３点の関数値から決める[4]）
このときのαを用いた

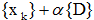
が新しい探索値となる。αの絶対値が十分小さいとき、与えられたΔに対する収斂とみなし、その移動量

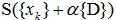
より材の伸縮量を計算し反力Ｒを求める。
そうでない場合には、次のステップへの準備として３種の計算をしておく。

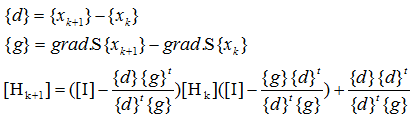
３番目がBFGS公式である。

ニュートン法ならヘシアンの逆行列を使うところであるが準ニュートン法では、このBFGS公式のような近似公式を用いるところがみそ。

一見複雑そうだが、そうでもない。右辺の分母はスカラーで同じ値だから一度の計算ですむ。
あとは対角行列や対称行列とベクトルの積だ。
逆行列の演算回数をザーッと変数の３乗レベルとすればこの公式では高々２乗レベルとなる。これは大きい。（べき乗の怖さは数値解析専門家だけでなく古くから知られている[5]）。

ここでｋ＝ｋ＋１と置き換えて前の10 CONTINUEに戻る。

図２の実線はこのようにして求めた結果だ。
BFGS公式以外にも色々提案されている[6～9]。例えばBFGS公式のほかDFP公式、ランク－１公式、Peasonの公式(図２では記号I～IV)、MacCormicの公式(記号V)、Powellの公式であり、この解析例ではI～IVがまあまあよさそうだ。

実は、ここまでは、ほんの入り口にすぎない。ここから先はいずれ又。
とりあえず石を3個ほど静かな池に投げ込んでおこう[10]。

  • 力の釣り合い式や変形の適合条件は一体どうなったの？
  • 積載荷重を想定した反力が負になるって根本的におかしいのでは？
  • 本当にこれでいいの？
参考文献
  1. Whittaker, E.T., "A treatise of the Analytical Dynamics of Particles and Rigid Bodies", Third Edition, Cambridge at the University Press, 1927, pp.245-262 では最小作用の原理が述べられている。
  2. Eizaburo Tachibana, "On application of the quasi-Newton method for structural analysis including the dynamic snap-through problem", Shells, Membranes and Space Frames, Proc. of IASS Symposium, 1986, Elsevier Science Publishers, Vol.3, pp.129-136
  3. 次の本に書かれているBASICのプログラムをみると、なーんだ関数のグラデュエントってこんな簡単に近似できるのか。目からウロコ。刀根さまさま。刀根薫、"BASIC"、プレイマイコンシリーズー１、培風館、1981、pp.198-207
  4. これについても[3]の文献で詳しく説明されている。
  5. 秀吉から好きな褒美をやると言われた曾呂利が、一日目は畳の一枚目に米粒を一粒、二日目は畳の二枚目にその倍の二粒、三日目はその倍の四粒、・・と倍づつ百畳分を所望した。秀吉はなーんだ、と言ったが、１００畳目は日本中の米粒でも足りない数になることが分かったという話が伝えられている。
  6. 今野浩、山下浩、"非線形計画法"、ORライブラリー６、1978、pp.196-216
  7. Huang H.Y.," Unified approach to quadratically convergent algorithms for function minimization", J.Optimization theory & Appl., 5, 1970, pp.405-423
  8. Denis J.E., More J.J.,"Qusi-Newton methods, motivation and theory", SIAM Review, 19, 1977, pp.46-89
  9. Powell G., Simons J., "Improved iteration strategy for nonlinear structure", Int. J. Num. Math. Eng., 17, 1981, pp.1455-1467
  10. 橘英三郎, "Snap-Through問題に含まれる衝撃荷重的な運動に関するメモ", 日本建築学会近畿支部、構造力学考究録、第７号、1990、pp.43-58 （これは、ＪＲ田町駅の近くにある日本建築学会の図書室で申込めば閲覧、複写などができる。ただし、会員以外は入室料300円也が必要。そこまで労力かける値打ちがあるのかと問われると、ウーン・・・、あ、震災がらみの貴重な資料も閲覧できますよ）
  • ※ 記載されている製品およびサービスの名称は、それぞれの所有者の商標または登録商標です。
すべての記事を見る

技術ブログカテゴリ

新着記事

トップへ戻る