グラフェンシートの分散性を考慮した熱伝導解析
PEEKマトリクスにグラフェンシートを添加したCFRTP(炭素繊維強化熱可塑性樹脂)の熱伝導特性を解析しました。散逸粒子動力学(DPD)を用いてグラフェンシートの分散構造を求め、得られた構造を用いてDigimat-FEの有限要素法(FEM)により熱伝導率を評価しました。分散状態と凝集状態の比較により、分散性が高い方が熱伝導性向上に寄与することを確認しました。得られた熱伝導率を均質化されたマトリクス成分として、CFRTP全体の熱伝導率をDigimat-MFの等価介在物理論で評価しました。
解析・利用例のポイント
- グラフェン分散構造の評価
- 有限要素法による熱伝導解析
- 等価介在物理論を用いたCFRTP全体の熱伝導性評価
グラフェン分散構造の予測
COGNACの散逸粒子動力学(DPD)を用いて、PEEKマトリクス中のグラフェンシートの分散構造を計算しました。グラフェンに親水性を付与するための表面改質を表現するため、粗視化粒子間の相互作用を変更してダイナミクス計算を実施しました。表面改質の有無による分散性の違いを確認できました(10~100nmスケール)。

グラフェン分散構造
有限要素法による熱伝導解析
前ステップで計算されたグラフェンシートの配置座標をDigimat-FEの入力値として用いて、メッシュ構造を作成し、Digimat-FEの有限要素法(FEM)ソルバーにより熱伝導性能を評価しました。グラフェンが分散している構造の方が高い熱伝導性を示しました。

有限要素法による熱伝導解析
等価介在物理論を用いたCFRTP全体の熱伝導性評価
Digimat-MFの等価介在物理論を用いて、CFRTPのUD材(一方向にカーボン繊維が配列)全体について、繊維配向に対して垂直方向の平均熱伝導率を計算しました(100μmスケール)。その際、マトリクス成分の熱伝導率は、前ステップの有限要素解析で得られた結果を均質化された物性値として用いました。結果として、マトリクス領域に存在するナノスケールのフィラー分散構造の違いが、材料全体の熱伝導性能に影響を及ぼすことを確認しました。
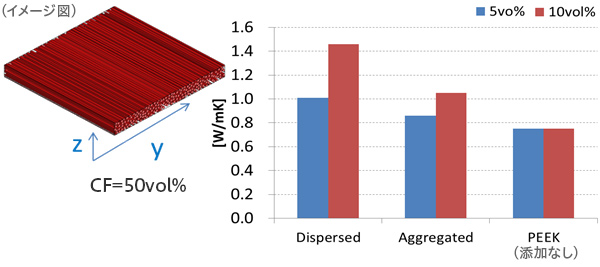
CFRTP全体の熱伝導性評価
参考文献
T.Ozawa, T.Nakayama, M.Watanabe, G.Goldbeck, V.Regnier, MOLMOD2015
解析内容の詳細