
CAE Technical Library エンジニアレポート - CAE技術情報ライブラリ
2010.05.06
コアの積層構造を維持するための手法として、圧入や焼き嵌めがあります。コアに電磁鋼板を使用しているモータの場合、圧入接合により発生した圧縮応力が鉄損を増加させることが知られており、鉄損解析において圧入応力を考慮することが重要になっています[1][2][3]。今回のNewsLetterでは、このような圧入応力の鉄損密度への影響を、LS-DYNAとJMAGとのカップリングシミュレーションによって評価する手法をご紹介します。
解析対象
今回は、図1、2および表1に示すようなSPMモータを解析対象とします。
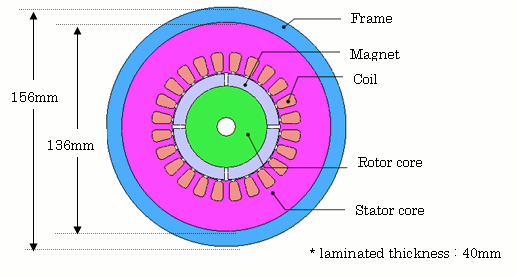 図1 解析対象
図1 解析対象
| 部品名 | 磁化特性 | 機械的物性 | その他 |
|---|---|---|---|
| ロータコア | 比透磁率: 新日鐵:50H600 |
- | - |
| 磁石 | リコイル比透磁率:1.05 保磁力:963(kA/m) |
- | 配向方向: パラレル円周パターン (図2参照) |
| ステータコア | 比透磁率: | 密度:8030(kg/m3) | 応力依存性損失特性: |
| B-Hカーブは図3参照 | ヤング率:1.197×1011(N/m2) ポアソン比:0.34 |
図4〜図7参照 | |
| フレーム | 比透磁率:1 | 密度:2710 (kg/m3) ヤング率:0.69×1011(N/m2) ポアソン比:0.28 |
- |
| コイル | 比透磁率:1 | - | - |
表1 各部品の物性値
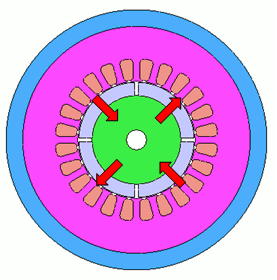 図2 磁石の配向方向
図2 磁石の配向方向
図3から図7に、B-H特性、およびコア損失特性の応力依存性を示します。後述するように、これらはJMAGでの鉄損解析で入力データとして使用します。
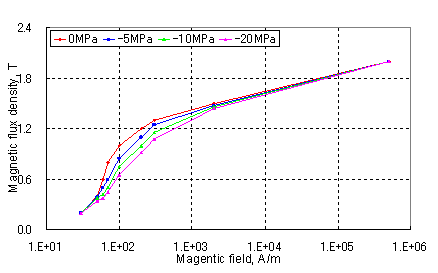 図3 応力依存性B-Hカーブ(ステータコア)
図3 応力依存性B-Hカーブ(ステータコア)
![図4 ステータコアの損失特性(応力:0 [MPa])](./img/e10002/e10002_04.gif) 図4 ステータコアの損失特性(応力:0 [MPa])
図4 ステータコアの損失特性(応力:0 [MPa])
![図5 ステータコアの損失特性(応力:−5 [MPa])](./img/e10002/e10002_05.gif) 図5 ステータコアの損失特性(応力:−5 [MPa])
図5 ステータコアの損失特性(応力:−5 [MPa])
![図6 ステータコアの損失特性(応力:−10 [MPa])](./img/e10002/e10002_06.gif) 図6 ステータコアの損失特性(応力:−10 [MPa])
図6 ステータコアの損失特性(応力:−10 [MPa])
![図7 ステータコアの損失特性(応力:−20 [MPa])](./img/e10002/e10002_07.gif) 図7 ステータコアの損失特性(応力:−20 [MPa])
図7 ステータコアの損失特性(応力:−20 [MPa])
解析フロー
解析フローの概要を図8に示します。はじめに、LS-DYNAを用いてステータコアとフレームとの圧入解析を行います。次に、解析結果(ステータコアの応力分布)をJMAGのPlotファイルフォーマットに変換します。最後に、JMAGで鉄損解析を実施します。
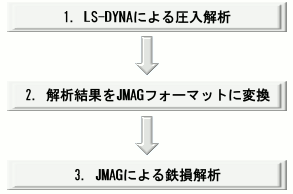 図8 解析フロー
図8 解析フロー
各フェーズの詳細を以下にまとめます。
1. LS-DYNAによる圧入解析
ステータコアとフレームのみを対象に、5面体要素でメッシュ分割し、かつ弾性体として定義しています。今回はモータ構造と変形の対称性を利用して4分の1モデルとします。
圧入解析手法として、*CONTACT_SURFACE_TO_SURFACE_INTERFERENCEを利用します。すなわち、ステータコアとフレームとを予め圧入代分だけめり込ませておき、動的緩和法によって両者間の反力を求めながらめり込みを除去します(図9)。動的緩和終了後、動解析を1サイクルだけ実行し、ステータコアのdynainファイルを取得します。得られたdynainファイルを次ステップのフォーマット変換に利用します。
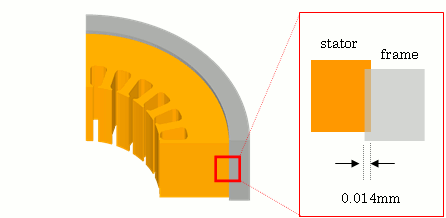 図9 ステータコアとフレーム間のめり込み
図9 ステータコアとフレーム間のめり込み
2. JMAGフォーマットへの変換
先に得られたdynainファイルを、JMAGのPlotファイルフォーマットに変換します。今回の検討では、perlスクリプトを作成して変換を実施しました。
3. JMAGによる鉄損解析
変換によって得られたPlotファイルを用いてJMAGで鉄損解析を行います。ただし、LS-DYNAで使用したメッシュデータは鉄損解析でそのまま使用することができないため、初めにJMAGの機能を用いて鉄損解析用メッシュデータに応力情報をマッピングします(図10)。
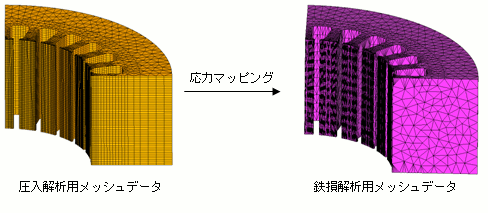 図10 各フェーズにおけるメッシュデータと応力マッピング
図10 各フェーズにおけるメッシュデータと応力マッピング
鉄損は磁界解析によって得られる磁束密度分布から求めます。図3から図7に示したような鉄損特性を予め設定しておくことで、磁界解析終了後に自動的に鉄損分布が計算されます。
解析結果
圧縮応力分布を図11に、主応力ベクトル分布を図12に示します。図11より、ヨーク部におけるスロットとの接触部において得に圧縮応力が大きくなっていることが分かります。図12の主応力ベクトル分布より、スロットとの接触部では圧縮応力が、フレームでは引張応力が支配的になっていることがわかります。
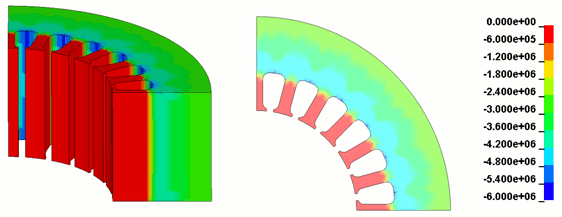 図11 圧入解析によって得られたコア内の圧縮応力分布(単位:Pa)
図11 圧入解析によって得られたコア内の圧縮応力分布(単位:Pa)
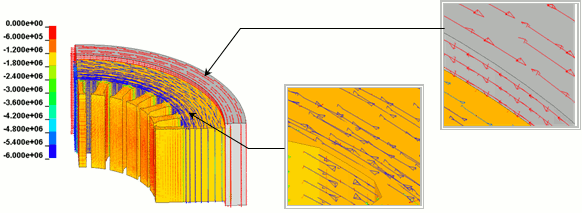 図12 主応力ベクトル分布(単位:Pa)
図12 主応力ベクトル分布(単位:Pa)
図13に、鉄損解析モデルへのマッピングされた応力分布を、図14に、最終的に得られた鉄損分布を示します。図14より、鉄損分布は圧入時の応力を考慮することで著しく変化しており、応力を考慮することで約12%鉄損が増加していることが確認できます。
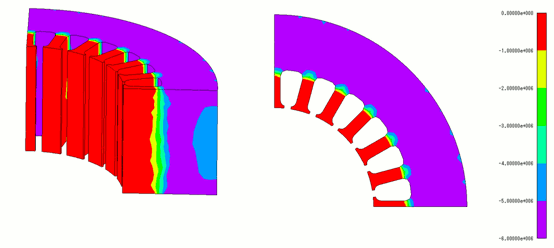 図13 マッピング後の応力分布(単位:Pa)
図13 マッピング後の応力分布(単位:Pa)
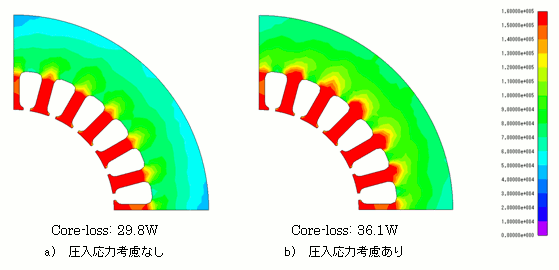 図14 鉄損密度分布(単位:W/m3)
図14 鉄損密度分布(単位:W/m3)
まとめ
圧入応力を考慮した鉄損評価を、LS-DYNAとJMAGとのカップリングシミュレーションで行う手法をご紹介しました。この手法を用いることで、圧入応力の鉄損分布に与える影響を明確に得ることが期待できます。また、LS-DYNAの熱応力解析機能を利用すれば、圧入のみならず焼嵌めへの適用も可能だと考えられます。
- 参考文献等
-
- [1] Hiroshi Fujimura, Hiroyoshi Yashiki, Hiroshi Kojima and Taisei Nakayama (Sumitomo Metal Industries, ltd.): Effect of shrink-fitting stress on ring core magnetic properties of non-oriented electrical steel sheet, The papers of Technical Meeting of Magnetics, IEE Japan, MAG-05-103, pp.1-6, 2005.
- [2] Hiroshi Fujimura, Hiroyoshi Yashiki, Hiroshi Kojima and Taisei Nakayama (Sumitomo Metal Industries, ltd.): Effect of interlocking shape on magnetic properties of non-oriented electrical steel ring core lamination, The papers of Technical Meeting of Magnetics, IEE Japan, MAG-06-138, pp.39-44, 2006.
- [3] JSOL Corporation: JMAG Application Note Iron Loss Analysis of an SPM Motor Including the Effect of Press-fitting Stress, http://www.jmag-international.com/catalog/





