
CAE Technical Library 吉田弾塑性工学塾 - CAE技術情報ライブラリ
2025.2.13
9.Yoshida-Uemori model(その3)
- 塑性力学、材料モデルの研究に魅せられて -
1.はじめに
先回のエッセーでは、Y-U model1)-3)は、降伏曲面が大きさ・形を変えずに、限界曲面の中を移動する移動硬化モデルであることを説明しました。限界曲面は、塑性変形とともに拡大し、同時にわずか移動硬化もします。今回は Y-U modelの移動硬化の具体的な表現について解説します。
2.A-F modelとY-U model
移動硬化(kinematic hardening)モデルとは、降伏曲面の中心 \(\alpha_{ ij } \) が塑性変形によってどのように変化するかの定式化です。これは背応力(backstress)の発展式とも呼ばれます。Y-U移動硬化モデルについて、先のエッセー「6.繰返し塑性モデル(その2:非線形移動硬化モデル)」でも紹介したArmstrong-Frederick (A-F) model4)と比較しながら解説します。A-F modelは次式で表されます。
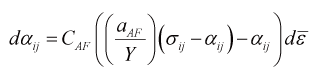
(1)
これは単軸応力状態では次のようになります。
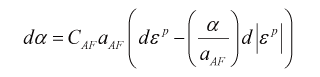
(2)
この右辺の第一項は線形移動硬化(背応力増分 \(da\) が塑性ひずみ増分 \(d\varepsilon^{p}\) の線形関数)の形になっていますが、第二項(これは動的回復項と呼ばれることがあります)があるため、塑性ひずみの進行とともに移動硬化の進行速度が遅く(すなわち硬化係数が小さく)なりますY-U modelでは、A-F modelと次の二点が異なっています。
-
 画像拡大
画像拡大
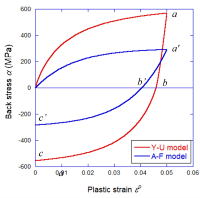
Fig.1 DP980高張力の応力反転時の移動硬化( \(\alpha\) の変化):A-F modelとY-U modelでの計算結果
-
 画像拡大
画像拡大
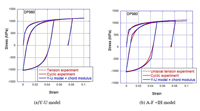
Fig.2 Y-U modelとA-F+IH modelで計算したDP980高張力の応力−ひずみ曲線((a)Y-U model 、(b)A-F +IH model)
- (1)降伏曲面の移動 \(\alpha_{ ij } \) は、限界曲面内の相対的移動 \(\alpha_{ ij }^{*} \) と限界曲面そのものの移動 \(\beta_{ij}\) の和として表されます(「8.Yoshida-Uemori model(その2)のFig. 4参照)
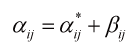
(3)
- (2) \(\alpha_{ ij }^{*} \) の移動硬化則では、次式に示すように、動的回復項がA-F modelとは異なっています。
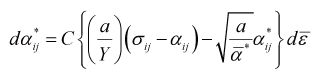
(4)
これは単軸応力状態では次のようになります。
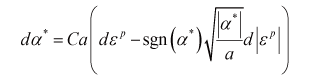
(5)
ここで、DP980高張力の応力反転時の移動硬化( \(\alpha\) の変化)をA-F modelとY-U modelで計算した結果をFig. 1に示します。Y-U modelでは応力反転開始(点a)から \(\alpha=0\) 点(点b)までの勾配 \(da | d\varepsilon^{p}\) がA-F modelのa’-b’における勾配よりはるかに大きいことがわかります。その結果、Y-U modelでは弾塑性遷移領域での応力−ひずみ挙動が実際の材料挙動により近く表現することができます。Fig. 2(a), (b)は、それぞれY-U modelとA-F+IH modelで計算したDP980高張力の応力−ひずみ曲線を示しています。
3.おわりに
今回は、Y-U modelの移動硬化則(backstress \(\alpha_{ ij } \) がどのように塑性変形とともに変化するか)について、A-F modelと比較しながら説明しました。次回は、Y-U modelの特徴である、応力反転直後に加工硬化が小さくなる現象(workhardening stagnation)のモデル化について解説します。
- ■参考文献■
-
- 1) Yoshida, F., Uemori, T., Fujiwara, K., 2002. Elastic-plastic behavior of steel sheets under in-plane cyclic tension-compression at large strain. International Journal of Plasticuty 18, pp.633-659.
- 2) Yoshida, F., Uemori, T., 2002. A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation. International Journal of Plasticity 18, pp.661-686.
- 3) Yoshida, F., Uemori, T., 2003. A model of large-strain cyclic plasticity and its application to springback simulation. International. Journal of Mechanical Sciences 45, pp.1687-1702.
- 4) Armstrong, P. J., Frederick, C. O., 1966. A mathematical representation of the multiaxial Bauschinger effect. GEGB report RD/B/N731. Berkley Nuclear Laboratories.
※記載されている製品およびサービスの名称は、それぞれの所有者の商標または登録商標です。


 株式会社JSOL エンジニアリング事業本部 技術顧問
株式会社JSOL エンジニアリング事業本部 技術顧問


