
CAE Technical Library エンジニアレポート - CAE技術情報ライブラリ
2012.08.01
工業力学の父チモシェンコの自伝から、材料力学が成長・発展した過程をうかがい知ることができます。激動のロシア革命から第二次大戦を経て93年の長寿をまっとうした人生(1878年-1972年)は、現在CAEにたずさわる私たちに有益な指針を与えてくれます。
鉄道のレールを見て考えること
凡人と偉人では、同じ軌道(レール、枕木、その下のバラスト)を見ても思いつくことが違います。浅学菲才の筆者は前職の習慣から、つい「枕木を間引いてコストダウンできないか、もっと間隔を広げて使用本数を減らせないか?」等を考えてしまいます。
 写真1 駅のホームから眺めた軌道(レール、枕木、バラスト)
写真1 駅のホームから眺めた軌道(レール、枕木、バラスト)
チモシェンコは「シベリア鉄道の軌道の合理的な設計指針を作成せよ。レールのたわみの計算方法を提案せよ。」という課題に対して、レールを「全長を連続的な弾性床に支えられている一様断面の梁」と考え、梁のたわみ曲線の微分方程式を応用して、以下の式を提案しました。
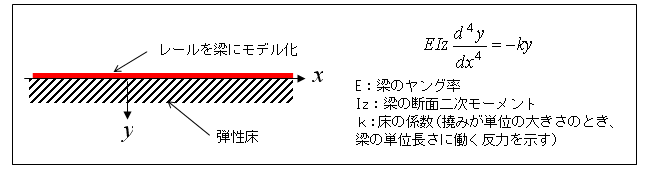 図1 弾性床上の梁
図1 弾性床上の梁
以下は、自伝1)からの引用です。
「・・・・相当連続弾性床を使って問題を単純化するという考えが私の頭に浮かんだ。予備計算をしてみると、軌道への集中応力はレールによって、ちょうど5本の枕木に分布されること、この数の支持ならば、それらを連続弾性床で置き換えてもレールの撓みや応力にはごく僅かの影響しかないことが判明した。レールの計算を弾性床上の梁の計算としてとらえることによって、問題の解を単純化することができた。・・・・」
モデル化の力を養うには
図1のような大胆なモデル化については、現在の鉄道土木の立場からいろいろ問題点を指摘されるかもしれません。しかし「第一次近似として、このようなモデルを提案する」という思想がCAEでも重要です。では、このモデル化の力をどのようにして養えばよいのでしょうか? 筆者は、教育訓練を積むことと思います。
チモシェンコは、単に思いつきで図1を提案したのではありません。膨大な実験データと文献を整理して、実用的な計算精度で使えるモデル化を行ったのです。若きチモシェンコが在籍した交通運輸専門学校では、基礎科学とともに実践的な教育トレーニングが行われました。たとえば、列車が通過する前後のレールの沈下量の測定、凍土に覆われたシベリア大陸のどこに駅舎・鉄橋を建設して、軌道をどのように敷設したらよいか企画立案、さらに建設作業者の監督指導も含めて、当時の学生は多くの課題をこなしました。正解のない課題を与えられて、限られた期間(夏休みの実習期間)で解決する訓練を受けたようです。全ロシアから選抜された俊才集団だからこそ、可能だったと思われます。
また、彼の思想の形成には父親の影響もあると思われます。彼の父親は勤勉な測量技師でした。ここでいう測量技師とは、単に土地の測量をするだけでなく凍土の地盤調査、住宅建設のアドバイスをしたり、はては、地主と小作人の間に入って調停業務をしたり、高範囲な仕事をこなす職業だったようです。父親を通じて彼は、もの心ついた時から「現実的な技術の重要性、人にものを分かりやすく説明するミュニケーションの重要性」を感じていたようです。
チモシェンコは、図1の考えを応用して様々な実際的な課題に具体的な解を示しています。たとえばレールが部分的に荷重を受けた場合、動的な荷重を受けた場合および枕木の影響等についても述べています。彼は、自分の理論と実際の現象との差が生じる原因を率直にあげて、最後に「しかし、このような理論は実用的に十分な精度を与える。一般的にこの計算方法は、従来の実験結果と一致する結果を与える」と結びます。
「この(簡単モデルによる)理論は、実用上、十分な精度を与える」という文は、彼の著書によく現れます。この言い回しは絶妙でCAEにも使えるかもしれません。しかし使用には注意が必要です。なぜなら、その根拠を求められたときの説明責任を伴うからです。
 図2 チモシェンコ著,材料力学(英語版,パート2の表紙)
図2 チモシェンコ著,材料力学(英語版,パート2の表紙)
日焼けした古い本ですが、筆者が学生時代に使ったものです。
- (注)原著(ロシア語、英語)は、パート1(初心者向け)とパート2(上級者向け)に分かれている。パート2の7章まで日本語訳が出版されているが、8章以後の日本語訳は未完。そこには応用的な内容(高温強度、疲労、破壊条件および応力測定実験等)がまとめられている。
最近の軌道解析
図1の式中のKは路面のたわみ易さを表す係数です。一般にこの値はFWD(Falling Weight Deflectometer)という装置で「錘を地面に落下させて、たわみを測定することにより求められます。土木の分野では、このFWD測定に関するFEM解析との比較研究が多くみられます。軌道モデルの場合、Kは「道床、バラスト(砕石、砂利)および枕木等」を含む相当たわみ係数を意味しています。
最近では、図3のように「車輪、レール、枕木およびバラスト等」を個別にモデル化した、より詳細なFEM解析も行われています。この解析目的は、車輪の変動荷重におよぼすレール継ぎ目の影響の調査2)で、使用コードはLS-DYNAです。
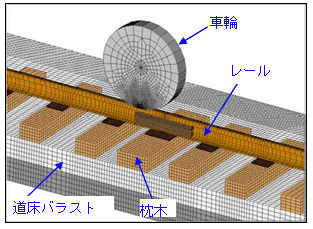 図3 FEMモデルの例2)
図3 FEMモデルの例2)
図4は、JSOLで行われた列車の走行シミュレーション3)の例で、カーブしたレール上を車輪が走行する状態を解析しています。このFEMによる厳密な接触解析により、レールの詳細な応力(図5)を求めることができます。
図4 LS-DYNAによる走行シミュレーション3)
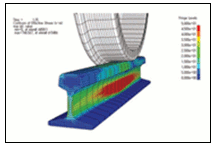 図5 レールの応力
図5 レールの応力
このように、最近はチモシェンコの梁理論を知らなくてもCAEツールにより、実際的な軌道解析ができるようになりました。解析人口が増えたことは良いことですが、現象の本質的なメカニズムを見抜く力の向上にも努めたいものです。
まとめ
シーナアイエンガーは、選択の科学4)で「専門家が初心者と違うのは、いろいろな選択を単純化、分類、優先順位づけができる点」をあげています。CAEの場合「いろいろな選択」を「解析モデル」に置き換えると分かりやすいでしょう。
実際の軌道を弾性床上の梁に置き換える(図1)というのは、見事な単純化の例です。チモシェンコは、材料力学の分野で多くの書物を残しました。彼が尊敬されるゆえんは、著書の内容が工学教育に関するものだからです。数学や物理学の原理的な内容を、いかにしてリアルな工学教育に落とし込むかがチモシェンコの課題であって、それに成功したことが自伝1)に述べられています。その基本的な考え方は、FEM全盛時代の現在でも通じるものがあると思います。
さて皆さんは、駅のホームで軌道を見て何を考えられるでしょうか?
筆者の紹介
徳満 祥三
株式会社JSOL エンジニアリングビジネス事業部 技術顧問。カヤバ工業株式会社(現KYB株式会社)にて、CAEの社内展開および製品開発支援に従事。2011年定年退職、現在に至る。
- 参考資料
-
- (1) チモシェンコ自伝(思い出すままに),著者:チモシェンコ,翻訳:田中勇,1978年,東京図書
- (2) 堀池高広,桃谷尚嗣:レール継目部沈下対策工法におけるレール圧力の解析,2005年土木学会第60回年次学術講演論文集
- (3) 伊田徹士,戸倉直:陽解法有限要素モデルによる列車走行シミュレーション,2005年機械学会,第15回設計工学システム部門講演論文集,154-155
- (4) 選択の科学、著者:シーナ・アイエンガー,翻訳:櫻井祐子,出版社:文藝春秋,発売日:2010年11月





