高張力ハイテン材などを曲げ加工する際にR部などで発生する加工硬化は、バウシンガー効果により移動硬化則に基づいて降伏曲面が応力履歴によって変化します。本稿では、バウシンガー効果による降伏曲面の変化を考慮可能な材料モデルを使用し、加工硬化を考慮したBピラーの衝突解析事例を紹介します。
移動硬化則による曲げ戻し工程の予測精度向上
本稿の対象となるBピラーは、ハット形状のドロー成形部品と仮定しています。つまり、Bピラーは、金型のR部に沿った引き込み曲げ(正方向の応力発生)、曲げ戻し(反転変形として反転方向塑性変形)、弾性除荷(スプリングバック)が繰り返し発生する弾塑性変形の影響を受けます。
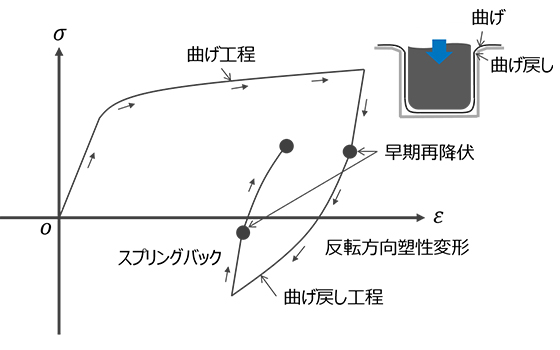
図1の曲げ戻しによる応力反転時における早期再降伏は、移動硬化による降伏曲面の中心が塑性変形とともに移動する現象で、その中心を背応力(Back stress)と呼びます。続いて硬化則について説明します。
等方硬化と移動硬化、複合硬化における背応力の変化
等方硬化では、塑性変形によって降伏曲面の大きさが変わりますが、降伏曲面の中心は変わりません。移動硬化は、塑性変形よって降伏曲面の形状は変わりませんが、降伏曲面の中心が変形とともに移動するという考え方です。そして降伏曲面の中心を背応力(α)と呼びます。これら2つの硬化則を複合させたのが複合硬化則で、降伏曲面の円の中心が移動し、かつ、降伏曲面の大きさも変化します。
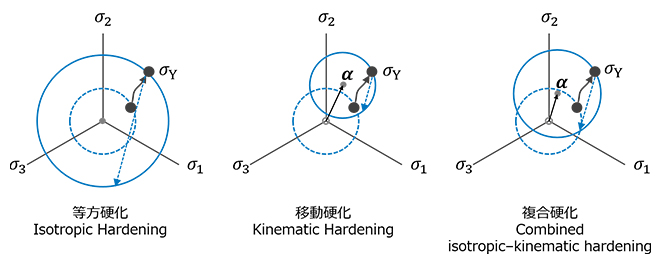
Ansys LS-DYNAにおいて広く使われるMAT024は図2左側の等方硬化則を、高精度な成形シミュレーションによく使われるYoshida-Uemori model(Y-U model)は複合硬化則を、それぞれ採用しています。
続いて、等方硬化モデルと複合硬化モデルとの違いを説明します。
移動硬化則によるバウシンガー効果の考慮と高張力鋼板の応力ひずみ曲線
図2の左グラフは、等方硬化モデルと移動硬化モデルそれぞれの曲げ戻しによる応力ひずみ曲線です。等方硬化モデルでは曲げで発生した正方向の応力の分だけ負方向に応力が進行しているのに対し、移動硬化モデルでは応力反転後の極めて早い段階で再降伏が起こり、その後、加工硬化率が急激に変化する遷移的バウシンガー効果に続いて永久軟化が起こります。
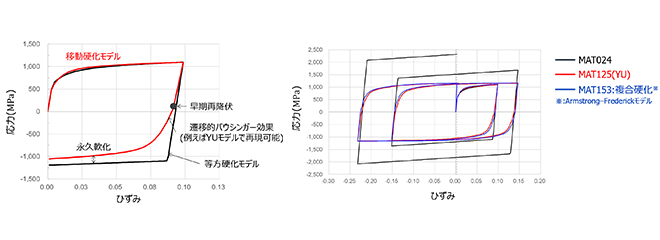
図3の右グラフでは、繰り返し塑性応力-ひずみ挙動について、等方硬化モデルであるMAT024と、複合硬化モデルであるY-U model(MAT125)およびArmstrong-Frederick model(MAT153)を比較しています。MAT024では、曲げ戻しが繰り返されることで応力が大きくなり続けるのに対し、2つの複合硬化モデルでは最大応力が一定の値で推移しています。 図3の右グラフに示すとおり、2つの複合硬化モデルが同様の応力-ひずみ曲線を示すことから、本稿では、より入力がシンプルなMAT153で検証を進めます。
初期塑性ひずみと背応力を考慮した板材およびハット材による複合硬化モデルの効果検証
図4のモデル図は、曲げ加工がされた板材の押しつぶし(曲げ戻し方向への変形)解析による荷重-変位曲線の違いを示しています。図4の右グラフは荷重-変位曲線を示します。移動硬化モデルであるMAT024では、加工硬化の影響を考慮する「初期ひずみあり」のケースの方が変形に対する荷重の増加が長く続いています。これは、等方硬化モデルでは初期ひずみにより正方向の応力をゼロに戻す分の荷重が含まれるためです。一方、複合硬化モデルであるMAT153では、荷重の増加は緩やかで、複合硬化モデルによる早期再降伏が発生しています。
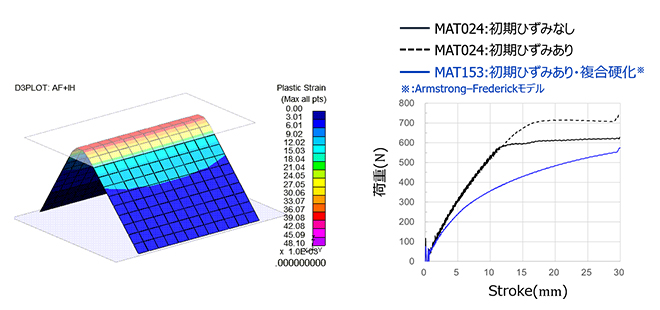
図5に示すとおり、ハット形状の押しつぶし(曲げ戻し方向への変形)も同様に、上部肩Rで曲げ戻しが発生しています。そのため、バウシンガー効果(背応力)を考慮するMAT153の方がMAT024よりも荷重が小さく出ています。
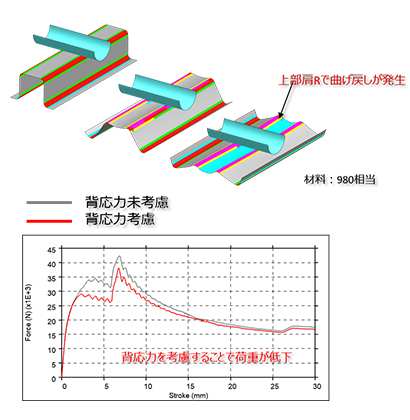
このように曲げが発生した箇所で曲げ戻し方向に変形が進む現象においては、複合硬化モデルを用いることで早期再降伏による荷重の低下が再現できます。
最後に、曲げ戻し方向への変形が発生する現象として、Bピラー衝突解析における移動硬化モデルを用いた検証例題を紹介します。
移動硬化則に基づくバウシンガー効果を考慮したBピラー衝突解析
使用するモデルは、CCSA※2の2012 Toyota CamryのBピラーモデルです。本稿では、Bピラーを対象に移動硬化モデルを用いたバウシンガー効果の考慮有無による荷重履歴の違いを比較します。
比較する事例では、等方性材料モデル(MAT024)、赤い丸で囲まれた部品に対してはバウシンガー効果を考慮可能な移動硬化モデル(MAT153)を使用し、両方ともHYCRASHにより加工硬化を考慮したひずみ分布を初期条件として与えます(図6)。
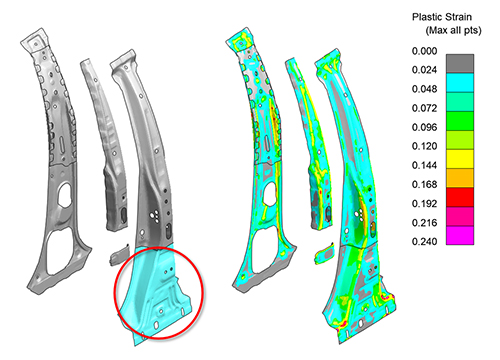
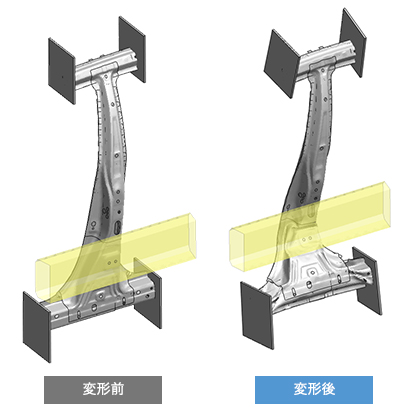
図8では、図7の衝突解析を実施した際の、荷重変位時刻歴グラフを示しています。障害物が衝突することによりBピラーが曲げ戻し方向に変形するため、MAT153ではMAT024に比べて荷重が低く、前述したハット型形状の押しつぶし解析の傾向とも一致していることがわかります。
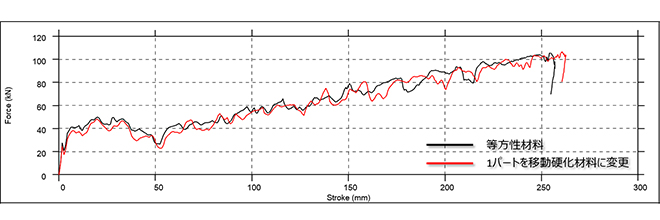
移動硬化則に基づくバウシンガー効果を考慮したBピラー衝突解析
本稿では、移動硬化則による曲げ戻し工程の変形予測精度向上を目的に、曲げ戻し工程における早期再降伏からスプリングバックによる応力緩和、等方硬化、移動硬化、複合硬化時の降伏曲面の形状および背応力の変化、移動硬化則によるバウシンガー効果から曲げ戻し方向への変形にともなう反力の低下と、Bピラー衝突解析における加工硬化の影響を考慮した移動硬化モデルによる荷重履歴への影響について紹介しました。
衝撃変形解析において反力が予想以上に大きく出ており、かつ、支配的な変形方向が曲げ戻し方向のときは、加工硬化の影響を考慮した移動硬化モデルを採用することで予測精度の向上につながる場合があります。
本稿にご興味がございましたら、お気軽に弊社担当営業もしくは、こちら までお問い合わせください。
- 成形シミュレーションの高精度化のための弾塑性構成モデル, 吉田総仁, 材料, vol.72, No.1, pp.67‐72, Jan. 2023
塑性学, 後藤學, 株式会社コロナ社, pp.55‐56, 1995年12月15日 - CCSA(Center for Collision Safety and Analysis ‐2012 Toyota Camry (gmu.edu))
この記事の関連情報
技術ブログカテゴリ
新着記事
- 分子シミュレーションで設計するプラスチックリサイクル
- 形状設計フェーズでの組み立て精度向上によるコスト削減
~ 組み立てCE検討ツールのご紹介 ~ - JSOLが考える「溶接シミュレーションと工場デジタルツインが実現する工程設計」について講演しました
- リアルワールドの自動車衝突安全に向けて
- 機械学習で加速する材料シミュレーション技術
- ノウハウ不要!樹脂の複雑な材料特性を簡単にフィッティング 〜 材料同定ツールと高精度ユーザーサブルーチンの活用事例 〜
- 樹脂材やゴム材の高精度予測に向けたパラメータ同定
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(後編)
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(前編)
- 製造業におけるマテリアルズ・インフォマティクス
