
CAE Technical Library エンジニアレポート - CAE技術情報ライブラリ
材料設計のために必要な電気伝導のシミュレーションには、対象の材料やスケール、電荷の種類に応じたバリエーションがあります。同一の電流経路であっても、着目する領域によって測定対象や評価方法が異なることがあります。たとえばバッテリーを考える場合、電解質領域はイオン電導であり、電極界面では電子伝導というように現象が異なります。このため、シミュレーションを利用した電気伝導現象の評価には、解析対象に応じて、有限要素法(FEM)、分子動力学(MD)、第一原理計算(DFT)などを用いたマルチスケール・シミュレーションが必要になります。
本稿では、表1に示すように対象のスケールと電荷の担い手に着目して、イオン伝導、電子伝導(パーコレーション/ホッピング伝導/バンド伝導/バリスティック伝導)をご紹介します。
バリスティック伝導を除く伝導現象については、系の電流密度 \(J\) は伝導度 \(σ\) と電場 \(E\) により次式で表されます。
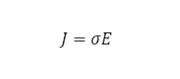
伝導度 \(σ\) は電荷量 \(q\) 、キャリア密度 \(n\) 、移動度 \(μ\) によって表されるため、各伝導現象において移動度に影響する因子に着目するとよいでしょう。

表1. 本稿で扱う伝導現象の種類/スケール/キャリア
| 伝導現象 | スケール | 電荷キャリア | 移動度に関係する因子 |
|---|---|---|---|
| 1. パーコレーション | 〜1\(μ\)m | 電子 | フィラーの体積分率、分散構造 |
| 2. イオン電導 | 〜数百nm | イオン | 拡散係数 |
| 3. ホッピング伝導 | 〜数十nm | 電子 | 電子移動積分、再配置エネルギー |
| 4. バンド伝導 | 〜数十nm | 電子 | バンドのエネルギー分散 |
| 5. バリスティック伝導 | 〜数nm | 電子 | 電子の透過係数 |
1.パーコレーション(メゾスケール・複合材料)
一般的なポリマーなどの絶縁物質に導電性フィラーを少しずつ混ぜていくと、フィラーによる電気伝導のネットワークが形成されて、ある割合を超えると抵抗率が急激に低下して電流が流れるようになります。この現象は電気伝導におけるパーコレーション現象と呼ばれます[1,2]。電気伝導は経路構成に関わらず、パスが通ると電流が流れるため、その変化は熱伝導などの他の現象に比べると前後の変化が顕著なものとなります。
パーコレーション伝導のシミュレーションは、伝導経路全体を対象として解析します。そのスケールは一般にメゾスケール(数10nm〜1\(μ\)m)になるため、解析手段としてはFEMなどの連続体モデルの手法が有効な手段となります。例として、絶縁体中に導電性フィラーがランダムに配置されたモデルにおける電気伝導性についてDigimat※で解析した結果を示します。フィラー配置の違いによる顕著な電気伝導率の変化とともに、パーコレーションが生じた時の電流経路を確認することができます(図1)。フィラー内におけるジュール損失密度の集中と局所発熱分布を確認することも可能です。
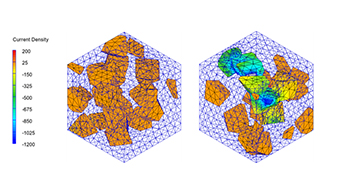 図1. Digimatを用いたパーコレーションの有無による電流分布と電気伝導への影響
図1. Digimatを用いたパーコレーションの有無による電流分布と電気伝導への影響
- 【関連ページ】
- カーボンナノチューブの分散構造と電気伝導性
2.イオン伝導(ナノスケール・イオンの拡散)
イオン伝導では、イオンの拡散現象の解析を通して電気伝導率を求めることができます。リチウムイオン電池を例に挙げると、解析から求められた拡散定数Dは、Einsteinの関係式(1)により移動度μに変換されて、最終的に電気伝導率が得られます。
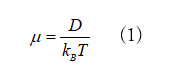
ここで、 \(k\)\(B\) はボルツマン因子、 \(T\) は温度です。
分子動力学シミュレーションを実行することにより、指定された分子または原子の平均二乗距離(MSD:Mean Square Distance)が求まり、拡散定数はその傾きから得られます。図2に液系電解質であるLiFSA(リチウムビス(フルオロスルホニル)イミド)と溶媒として炭酸プロピレン(PC)から構成される電解質溶液のモル分率比率に対する拡散定数と電気伝導率を示します。この結果から、LiイオンのMSDは電解質濃度とともに減少傾向を示すことが分かります。これは電解質の割合が大きくなるにつれて正負イオンによる再凝集が生じ、イオン伝導に寄与しなくなるためと考えられます。これに対して電気伝導度は電解質のモル濃度にも比例するため、本解析では緩やかに増加する結果が得られました。
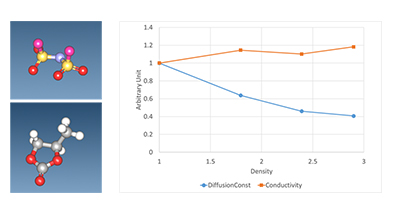 図2. FSAイオン(左上図)と炭酸プロピレン(PC)(左下図)とモル濃度ごとのLiFSA+PC系のLiイオンの拡散定数とイオン伝導率
図2. FSAイオン(左上図)と炭酸プロピレン(PC)(左下図)とモル濃度ごとのLiFSA+PC系のLiイオンの拡散定数とイオン伝導率
(LiFSAとPCの比率は1:6/1:3/1:2/2:3、縦軸は1:6の結果で規格化した無次元値)
LiZr2(PO4)3は、硫化物系固体電解質と並んで全固体電池への利用が期待されている酸化物系固体電解質の1つです(図3)[3]。液系電解質と同様にLiイオンの拡散定数の評価がイオン伝導度を決める指標になりますが、有機系を中心とした液系電解質と異なり無機材料から構成されるため、力場を利用した解析が困難です。このため、解析による評価にはDFT法などの第一原理計算が必要となります。
第一原理計算は、解析対象の組成と構造を決定すれば、電荷を含む力場の仮定を置くことなく計算を進めることができるため、有効な解析手段です(図3)。ただし古典分子動力学計算に比べて計算コストが高くなります。とくに拡散定数を評価するための緩和計算においては、ナノ秒オーダーの解析が必要とされることから、高並列計算機を使用しても1か月以上かかる計算も珍しくありません。近年は、機械学習を利用した解析の高速化技術により、第一原理計算を含むMD解析結果を利用した長時間の分子運動を予測、評価も可能になっています[4]。
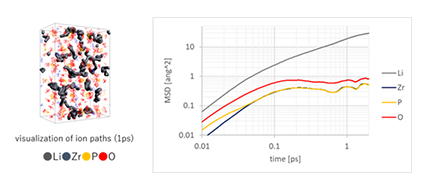 図3. LiZr2(PO4)3の各原子の移動履歴(太線がLiイオンの軌跡)と
図3. LiZr2(PO4)3の各原子の移動履歴(太線がLiイオンの軌跡)と
MSD(MSD:平均二乗距離、Liイオンの運動性評価)
- 【関連ページ】
- MD-GANによる固体電池内のLiイオン拡散解析
3.ホッピング伝導(ナノスケール・アモルファスの有機系)
ホッピング伝導は、不純物やアモルファス材料における電気伝導現象として知られています。有機ELなどの有機半導体を例に挙げると、ホッピング伝導により分子間(それぞれの分子に局在する軌道間)を電子が移動します(図4)。ホッピング伝導は次節で紹介するバンド伝導よりも移動度は遅くなりますが、有機半導体においてホッピング伝導が支配的であると考えられています[5]。
ホッピング伝導の理論としては古くからMarcusの理論が知られており、移動度 \(μ\) は電子移動速度 \(k\) により次のような式で表されます[6]。
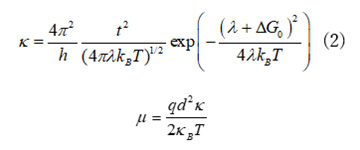
ここで、 \(t\) は移動積分、 \(λ\) は再配置エネルギー、\(ΔG\)\(0\) は始状態と終状態のエネルギー差、 \(k\)\(B\) はボルツマン定数、 \(T\) は温度、\(h\) はPlanck定数です。これに関して、分子論的に再配置エネルギー\(λ\) と移動積分(Transfer Integral) \(t\) を計算することが行われています[7,8]。 \(λ\) と \(ΔG\)\(0\) は以下の図4(右)に示すように、電子移動前後の2つの状態のエネルギー曲線と関係しています。 電子移動の前は、中性分子とイオン化した分子があり(エネルギー図のE1)、移動後には中性分子はイオン化しイオン化状態の分子は中性状態になります(エネルギー図のE2)。再配置エネルギーは、中性状態とイオン化状態のエネルギー差から計算することができます。移動積分の計算方法としては分子軌道をベースにした手法があり[8]、J-OCTAに同梱されているABINIT-MPにも電荷移動計算機能が実装されています[9]。 このようにして計算された移動度を用いて、デバイス中の電荷移動について動的モンテカルロによって計算された研究もあり[10]、材料開発で応用されています。
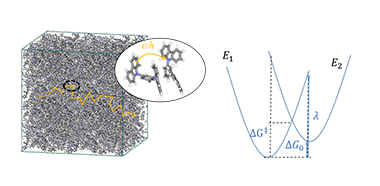 図4.(左)有機分子におけるホッピング伝導のイメージ
図4.(左)有機分子におけるホッピング伝導のイメージ
(右)ホッピングによる電子移動反応前(E1)と後(E2)の状態に対するエネルギー曲線
4.バンド伝導(ナノスケール・結晶)
金属などの無機結晶における電気伝導はバンド伝導と呼ばれます。これらの結晶中の電子は前節と異なり非局在化され、連続的とみなせる波数とエネルギーの分散関係を示すエネルギーバンドを形成します。エネルギーバンドは1つの波数に対して複数存在します。結晶の電気伝導性はエネルギーバンドを通して確認することができます。図5に例を示しました。金属であるCuではFermi準位がバンド曲線と交点を持ち、一番高い準位(Fermi準位)にある電子はすぐ上の準位に励起することができるため、電気伝導性を示します。一方、絶縁体(半導体)であるSiでは電子が完全に詰まったバンド(価電子帯)とその上の空いたバンド(伝導帯)に分かれて存在します。このギャップの存在により、電子が伝導帯に遷移して伝導性を示すには熱や光などのエネルギーを加えるか、不純物によってキャリアを導入する必要があります。
このような材料における電気伝導率 \(σ\) の具体的な表式は、量子論が誕生する以前にDrudeにより与えられました。バンド伝導において移動度は
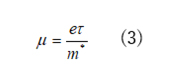
ここで、 \(e\) / \(m\)\(∗\) / \(τ\) はそれぞれ電荷/有効質量/平均自由行程時間を表します。この式は量子力学的にも求めることが可能であり、その妥当性が確認されています。
上記の式から電子の平均自由行程時間 \(τ\) が電気伝導率 \(σ\) を決める上で重要となりますが、 \(τ\) はおもに結晶の欠陥や境界などの幾何形状に由来する電子の弾性散乱や原子振動による非弾性散乱により決定されます。また有効質量 \(m\)\(∗\) は真空の電子質量とは異なり、結晶の原子構造を反映した値になります。バンド理論ではエネルギーバンドの曲率から求められます。
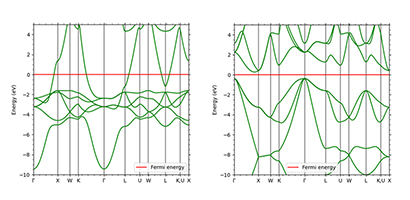 図5. Cu(左)とSi(右)のバンド図の比較
図5. Cu(左)とSi(右)のバンド図の比較
- 【関連ページ】
- LDA+U法による半導体バンドギャップの補正事例
5.バリスティック伝導(ナノスケール)
現在では、半導体の微細加工技術の進展などにより、ナノスケールレベルの形状を制御することができます。このような微小領域では、とくに低温下において(フォノンなどによる)電子散乱のない弾性(バリスティック)伝導が生じます(図6)。
SIESTA/TranSIESTAは、第一原理計算に基づく非平衡電流を扱えるので、電極と分子の境界での散乱の効果を含めたバリスティック伝導の解析が可能です。解析のためには非平衡グリーン関数(NEGF)法が実装されており、さまざまな伝導計算に適用可能です。

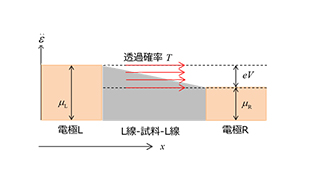 図6. リード線に繋がれた試料内におけるバリスティック伝導
図6. リード線に繋がれた試料内におけるバリスティック伝導
(バリスティック伝導では試料内散乱がないため、透過確率 \(T\) は1とみなせる)
さらに本手法は、そのほかにもさまざまなセンサー型デバイスの研究開発に用いられています。1つ目の例はNbSeTe単層デバイスにおけるガス分子のセンシングの研究例です[11]。図7には本解析に用いたモデルと、ガス分子が吸着した際のI-V特性の違いが示されています。もう1つの例はDNAシーケンサのシミュレーションです。図8にはグラフェン/h-BNの間に多くの水分子と1つの核酸分子が挟まれた構造において、NEGF法による電子輸送の計算が実施された例を示します[12]。上述のホッピング伝導などとの違いに興味が持たれますが、これらは高感度なセンサーの特性解析としてNEGF法を適用した面白い事例でしょう。
![図7. さまざまなガスを検知するデバイスのI-V特性の解析事例(文献[11])](./img/e24002/e24002-07.jpg) 図7. さまざまなガスを検知するデバイスのI-V特性の解析事例(文献[11])
図7. さまざまなガスを検知するデバイスのI-V特性の解析事例(文献[11])
![図8. NEGF法を利用したDNAシーケンサの解析モデル例(文献[12])解析に使用した核酸塩基(a)とナノ細孔への配置(b〜g)](./img/e24002/e24002-08.jpg) 図8. NEGF法を利用したDNAシーケンサの解析モデル例(文献[12])
図8. NEGF法を利用したDNAシーケンサの解析モデル例(文献[12])
解析に使用した核酸塩基(a)とナノ細孔への配置(b〜g)
6.おわりに
電気伝導現象は、測定の対象が多様で、かつ、スケールも極めて広範囲にわたります。今後も新しいデバイスや計測技術が開発されることで、電気伝導現象に求められる評価内容もさらに広がっていくと考えられます。シミュレーション技術もこれらの歩みに応じて進化していくでしょう。今後もJSOLは、最新の技術動向を分かりやすく解説し提供するよう努めて参ります。
(参考)エネルギーバンドとバンド伝導についての補足
図9の左図は、Na金属の格子定数(原子間の距離)を本来の値から5倍に設定した時の横軸を波数ベクトルに採った時のエネルギーの分散関係を表しています。横軸の波数に関わらず、一定の線スペクトルを示しており、それぞれNa金属の3s軌道とその上の三重に縮退した3p軌道を示し、その一番高いエネルギー準位を持った価電子は3s軌道に入ります(電子の局在化)。これに対して図9の右図は本来の格子定数に設定した状態であり、各軌道は連続とみなせる有限の幅をもったバンドを形成します(電子の非局在化)。Na金属の状態では3sバンドを半分だけ充填した状態となり、一番高い準位にある電子はすぐ上の準位に励起することができるため、電気伝導性を示します。このようにバンドに占める価電子との関係で決定される電気伝導をバンド伝導と呼びます。
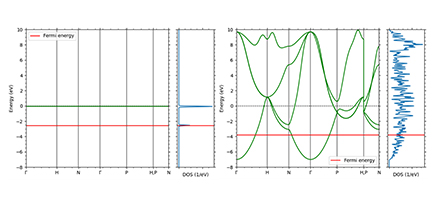 図9. Naの準孤立原子状態(左)と金属状態(右)
図9. Naの準孤立原子状態(左)と金属状態(右)
(左図は格子定数を5倍にして計算)
※Digimatの開発元はHexagon社のManufacturing Intelligence divisionであるe-Xstream engineeringです。
- 参考文献
-
- [1] S. Kirkpatrick, Rev. Mod. Phys., 1973, 45, 574
- [2] T. Ota, M. Fukushima, Y. Ishigure, H. Unuma, M. Takahashi, Y. Hikichi, J. Mater. Sci. Lett., 1997, 6, 1182
- [3] Y. Noda, K. Nakano, H. Takeda, M. Kotobuki, L. Lu, and M. Nakayama, Chem. Mater. 2017, 29, 8983-8991
- [4] 遠藤, 湯原, 泰岡, アンサンブル, 2019, 21, 39
- [5] A. Miller., E. Abrahams, Phys. Rev. 1960, 120, 745
- [6] R. A. Marcus; N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265; T. P. Nguyen, J. H. Shim, J. Y. Lee, J. Phys. Chem. C, 2015, 119, 11301
- [7] J. Blumberger, Chem. Rev., 2015 115, 11191
- [8] E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman, and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882
- [9] T. Fujita and Y. Mochizuki, J. Phys. Chem. A, 2018, 122, 3886
- [10] F. Suzuki et al., J. Mater. Chem. C, 2015, 3, 5549
- [11] D. Singh and R. Ahuja, Nanomaterials, 2020, 10, 2554;
- [12] F. A. L. de Souza, G. Sivaraman, M. Fyta, R. H. Scheicher, W. L. Scopel and D. G. Amorim: Nanoscale, 2020, 12, 18289-18295
- [13] B. J. van Wees, H, van Houten, C. W. J. Beenakker, J. G. Williamson, L. P. Kouwenhoven, D. van der Marel and C. T. Foxon: Phys. Rev. Lett. 1988, 60, 848
- [14] “Nanowires” edited by P.A. Serena and N. Garcia (NATO ASI series, Series E, Applied sciences ; no. 340) Kluwer Academic Pub., c1997
- [15] D. V. Averin and K. K. Likharev, “Mesoscopic Phenomena in Solids”, edited by B.L. Altshuler, P.A. Lee, and R.A. Webb (Elsevier, Amsterdam, 1991)





