
CAE Technical Library 注目機能紹介 - CAE技術情報ライブラリ
2009.02.02
構造物の挙動をシミュレートする構造解析においてLS-DYNAでは特に衝突や落下、回転、走行など動的な現象において多くの実績があります。一方、現象時間の長い静的/準静的な現象はマススケーリングなどを用いたり現象速度を仮想的に速めたりする解析テクニックを用いることに加え、Version 950より導入された陰解法ソルバーにより、強度解析や加工解析など、適用範囲を大きく広げました。
さらに、これらの静的な現象をシミュレートする解析テクニックや機能は、 一連の現象をより精度よく再現するために、動的解析と組みあわせて使われるようになりました。たとえば、自動車の衝突解析を実施するに当たり、重力下でのつりあい状態を求めることは、各部品の位置関係をより実機に近く配置するためには非常に重要です。また、携帯電話の中にある緩衝材が、アセンブリ時に圧縮されている場合、落下時の筐体の挙動を再現するには、その初期応力を正しく入力する必要があります。陰解法/陽解法スイッチや、動的緩和法を用いることにより、これらの一連の解析を結合し、実施することにより精度向上が図られてきました。
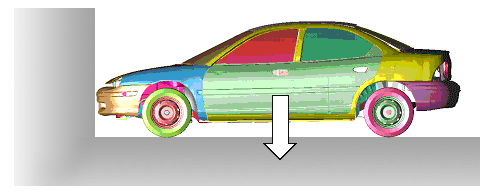 重力でのつりあいを求めたあと、衝突解析
重力でのつりあいを求めたあと、衝突解析
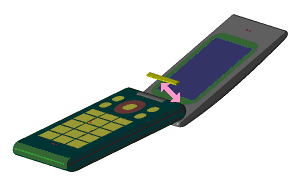 緩衝材の貼付、アセンブリの後、落下解析
緩衝材の貼付、アセンブリの後、落下解析
Steady State Rolling機能の背景
一方、これらの機能は静的なつりあい状態を求めるものではありますが、回転している物体のつりあい状態など、静的ではないが定常にある状態を求める場合、新しいアプローチが必要です。たとえば自動車を、ハンドルを切って旋回させる解析を実施する場合、まずは重力下で直進している状態を再現する必要がありますが。このとき、タイヤは自動車の重量で変形し、かつ、回転しています。この場合、タイヤは回転速度を持っており、通常の静的なつりあい状態を解く陰解法などではその状態を求めることはできません。しかし一般的に、このつりあい状態を解くだけで、実際に検証したい旋回解析以上の計算時間がかかることもあり、大きな課題のひとつでした。この、回転体の定常状態を再現するために開発された機能がSteady State Rolling機能です。
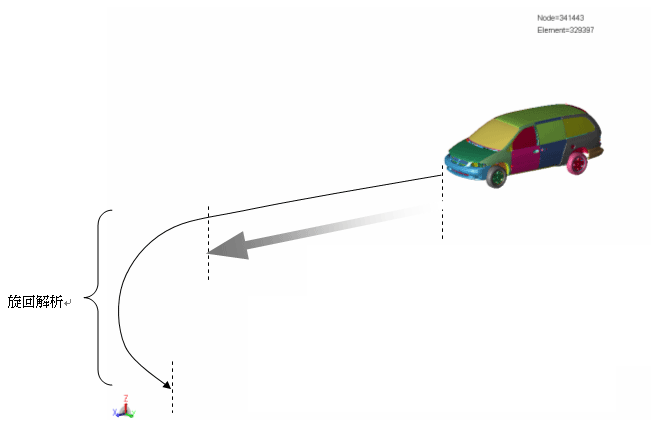 重力下での直進定常状態の再現
重力下での直進定常状態の再現
(設計上、検討したい現象(旋回)を再現するための前段階の解析であるが、計算コスト大)
Steady State Rolling機能の詳細および検証
Steady State Rolling機能のポイントは、回転体の回転方向とそれ以外の方法を別々の方式で解くところです。ここでは回転体としてタイヤを例にとって説明します。 タイヤの設置面は摩擦により発生する横力、前後力によりゴムブロックが変形していますが、その変形により応力が発生し、つりあっています。これだけであれば、通常の陰解法などの静的解析手法で解くことができますが、定常回転状態であるタイヤでは、摩擦力はゴムブロックの路面に対する相対速度(LS-DYNAで解析する場合は節点の速度)に依存します。
そこでLS-DYNAでは、ALE(Arbitrary Lagrangian and Eulerian)法を用い、回転方向とそれ以外の方法を分離します。ALE法とは形状の変化がそのまま変形を表すラグランジュ要素(Lagrangian element)と、要素は空間に固定し、要素・節点に付随する物理量の変化を計算するオイラー要素(Eulerian element)を組み合わせて解析する手法です。このSteady State Rolling機能では、回転方向をEuler要素で、それ以外の方向をLagrange要素で計算します。したがって、Steady State Rolling機能で計算をしている場合は、見た目上回転方向には節点は移動しません。
定常状態で回転しているタイヤは、軸周りの回転運動を除くと一定状態の変形を保って静止した状態に見えます。つまり、回転運動を除くと回転体の定常状態は、時間に依存しない静的な状態として解くことができ、計算が非常に効率的になるのです。
それではどうやって節点の速度を求めているのでしょうか?
Steady State Rolling機能では、回転が定常状態、すなわち回転速度が一定であることを前提にしています。そうすると、回転方向に並んでいる二つの節点の間の位置関係が、その間の節点の速度方向になります。
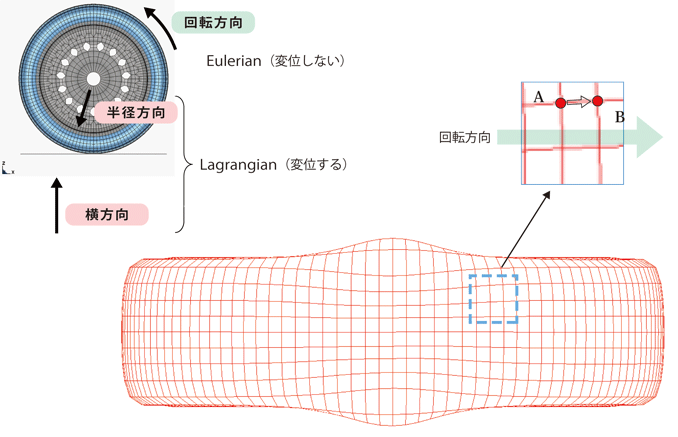
たとえば上図で、ある時間経過後、節点Aは節点Bに進むことが予測されます。Steady State Rolling計算は静的に解かれますが、回転方向の先にある節点Bによりその速度と方向を取得することができます。一方、回転以外の方向(半径方向、横方向)については通常のラグランジュ要素として変位し、応力を発生させます。
この結果、定常回転を行っているタイヤにおいて、そのつりあいの位置を求めることができます。この計算は各荷重ステップでつりあいを求めていく陰解法で行われるため、実際にタイヤを回転させていき、重力下での直進状態を求める従来の方法に比べて、圧倒的に計算時間を短縮できます。
この機能の検証のため、従来用いてきた陽解法での計算との比較を行いました。単体のタイヤを、自由転動(前後力が発生しない状態)にて各方向の力、および接触力の分布を比較しました。なお、Steady State Rollingでは入力値は荷重ではなく、角速度です。したがって自由転動状態を再現するためには、いくつかの角速度で計算し、前後力が0となる状態を探す必要があります。

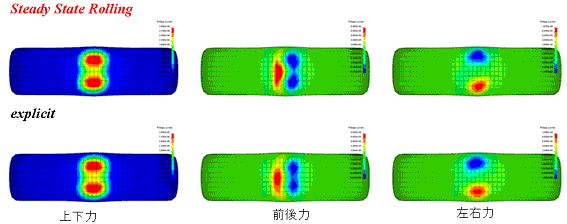 自由転勤における接触力分布の比較
自由転勤における接触力分布の比較
上記のとおり、従来用いてきた陽解法とほぼ同等の結果が得られています。
適用分野
Steady State Rollingは、ここであげたタイヤの転動解析を最初のターゲットとして開発されました。その特徴を用いれば以下の現象を解くことができます。
- 回転体である(回転方向に一様である)
- 変形する
- 速度を持っており、その速度が境界条件に影響する(摩擦など)
自動車のタイヤだけではなく、プリンターローラー、車輪、ベアリング、ハードディスクなど、多くの回転体の挙動の分析、設計などに用いることができます。

なお、本記事で用いたSteady State Rolling機能の例題は、解説およびキーワードマニュアルとともにユーザーサポートサイトからダウンロードできます。ユーザーサポートサイトの入力ファイルサンプル集からSteady State Rollingを検索していただくか、No.145 をクリックしてください。(ユーザーサポートサイトの閲覧には弊社ユーザーIDが必要です。)





