vol.20連続体（Continuum）って？

ここに天然水のペットボトルがある。この天然水は流体（Fluid）だろうか？それの置かれている机は固体(Solid)だろうか。実は、この質問は力学的にはあまり意味がない。というのもFluid や Solid は頭の中で考えられた力学モデルだからだ。そして、連続体（Continuum）もそれら２つのモデルを統合した力学モデルと言うことができる。これら力学モデルは、見かけとは関係なく、対象の挙動を表すのに都合の良いものが用いられる。たとえば、群衆の動きなどを予測する場合には流体として見做すことだってできる。ところで、力学モデルとはいえ用語が全てきっちりしている訳ではない。あちらこちらに怪しげなところもある。

質量密度について考えてみよう。ある点 ｐ の近傍で境界面 Γ （ガンマ）に囲まれた領域Ω （オメガ）を考える。その体積を ｖ とし、その質量を ｍ とすると、その付近の「平均」密度ρ （ロー）は　ｍ／ｖ としてよいであろう。ここで境界面 Γ を点 ｐ を囲むようにとりながらどんどんと小さくしていく。やがて周りの風景は分子がうごめいている世界に変わる。一見、一様に見えても金魚すくいの金魚のように領域Ω が分子を沢山すくえるときもあれば少ししかすくえないときもある。したがって運不運？により　ｍ／ｖ　は変動するであろう。しかし流体や固体では無限に領域を小さくしても一定の値に収斂すると仮定する。というよりは、分子や原子レベルの大きさまでは小さくしない領域にとどめて点ｐ 近傍の密度とする。分子間力と関わる応力や分子間距離の増分率に関わる歪についても同様である。「ある点における歪」などの言葉は平気で用いるが「点」は位置だけで長さや大きさはない。長さや大きさのないものにどうして歪が生じるのだ？　数学的な極限小が物理的に意味しない対象に、変位の偏微分を歪と定義するのは変ではないか・・となる。まあ、そうかたい話は抜きにして次に進もう。

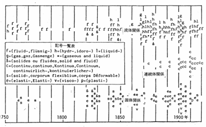
ところで 下図をみていただきたい。Truesdell の挙げた引用論文の題名で[1]、流体、固体、連続体に関する語の頭文字を年代順に並べたものである。（30年ほど前にタイプで打ったものをスキャンしたので、すこし見づらくなったがご容赦のほどを）

• 画像拡大

  Truesdell の挙げた引用論文の題名で、流体、固体、連続体に関する語の頭文字を年代順に並べたもの

図の上側にパラパラとあるのが流体関連の頭文字である。f、h、i、l、ｇ はそれぞれ fruid、frussig- 、hidoro-、idoro- liquid、gas、gaz、gaseousなどに対応する。又、下側の　s、e、v、pは固体関連の頭文字であり、solid、corporus、 flexibrium、corps、 elastic-、 Elasti-、 visco-、 plasti-、などに対応する。1800年前後が少ないのは、ナポレオンが恐妻ジョセフィーヌによるストレス発散のため？あっちこっちヨーロッパ中を暴れまわっていたせいかも知れない。

ところで、1870年代から中間層あたりに「c」 の頭文字が現れはじめる。それらはcontinu、continuo、Kontinua、continuum、continuerich-　などの頭文字である。これが「連続体」の出はじめであろう。少し紛らわしいのは、数学の分野にも連続体という言葉があることだ。全ての実数の集合などを表す。H, Weyl が自著の "Das Kontinuum"（1917）のp.65で mathematisches Kontinuum とわざわざことわって慎重に用いているところから、その当時は既に力学でのcontinuum が優勢であったのではなかろうか。

Y.C.Fung の "A first course in continuum mechanics" (1969）のp.2で The concept of a continuum is derived from mathematics. とあるが一概にどっちが先とも言えない。少なくとも目指していた方向が異なる。力学の場合は流体や固体などを統一的に扱おうとする意図が見える。一方、数学の場合は、実数全体や自然数全体の無限個からなる集合は、同じ無限個でも濃さ（濃度）が違うといったことや、両者の中間的な濃さはない、といった禅問答のような議論につながる方向だ。勿論、力学の連続体も実数軸で与えられた空間での議論だと言ってしまえば、そりゃー関係ないこともないが・・。

結局のところ、P.G.Hodge,Jr の "continuum mechanics" (1970）で序文に、Although it is only since about 1960 that the word "continnum" appears to have become popular in the engineering literature, the subject matter is as old as engineering. といったところが、どうやら正しそうである。

なお、continnumは continuous medium　からの縮約語であることは L.E.Malvern の "Introduction to the mechanics of a continuous medium"（1966）を持ち出すまでもなく、誰しも納得できるところであろう。

実は、この稿の表題は「離散系」のテーマで書くつもりだった。しかし、まず「連続体」に触れねば・・と思い書き始めると後戻りできなくなり（あっちこっち端折った荒っぽい話ではあるが）、ま、これでもいいか、となった次第だ。「離散系」については、いずれ又。