連続体(Continuum) については既に少しふれた。これ以上に固い話を続けると寛容な読者に見限られそうで不安でもある。とはいえもう少し・・。
連続体と対比されるモデルに離散系がある。質点系もニュートン型離散系などと呼ばれたりする。離散系でなくLagrange流に多自由度系という言い方もある。ではなぜ離散系などと言う言葉を使うのだろう?
その理由は思うに「連続」ときたら「離散」、continuousときたら discreteだ。以上終わり。
しかし、たった6行程度ではコラムのていをなさない。もっとこだわりたい方は GO TO 10。
10 CONTINUE
力学モデルにdiscrete を使った研究者を2,3列挙してみる。
| discrete system | by W.R.Spiller, Applied Mechanics Review 1971 |
| discrete models | by D.Greenspan, Addison-Wesley, 1973 |
| discrete parameter structural system | by K.J.Bathe, ASCE, EM3, 1973 |
もちろん他にも山ほどある。もっと古いところでさがしてみたら・・ |
|
| Systeme discreter Punkte | by P.Stäckel, Encyklopädie Mathematischen Wissenschäften, Teubner, Bd.4/4, 1905, p.473 |
これは、一部皮表紙で金文字の立派な本である。この中身は解析力学における多自由度系を述べている[1]。
そして、さらにもっとこだわりたい方は GO TO 20
20 CONTINUE
離散系には、いったん連続体にモデル化し、FEMにより離散化されたモデル(Discretized Model)も含む。よく知られているように離散系の釣合い点近傍の微小運動は次式であらわされる。
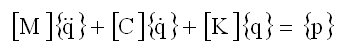
ここで、[M] は質量行列、[C] は減衰行列、[K] は剛性行列で {q}と{p}はそれぞれ一般化座標、一般化外力。ここで{q}は節点変位ベクトルでもよいが、それでなくても系の形状を一義的に定めるパラメータであればよく(それは、つまり一般化座標:generalized coordinatesと呼ばれるもの)、たわみ角法の部材回転角が含まれていてもよい。では変形パラメータのようなものになぜ「座標」とつけるのだろう?
それは、本コラムでちらっと触れている。その部分を再録しよう。
今、仮に水平変位だけ(これは誤りで、一方向の変位だけ)生じる2質点系を考える。その変位をd1、d2で表す。すると2質点系のすべての状態はd1、d2を座標とする平面上の1点で表される。20質点系ならd1、d2・・・、d20の20次元空間の1点となる。(2009年11月12日の「エネルギー誤差の分かっている近似解の話」より)
敢えて再録したのは、なぜ「座標」という言葉がつくのか?といった疑問に答える専門書が少ないからだ。さらに追い討ちをかけよう。n-次元空間の点の一般化座標方向の力の釣合い式は、Lagrangeの運動方程式により同一形式で与えられる。n-自由度系が、n-次元空間の一点に凝縮されたことになる。なんとエレガントな考え方であろう。
ところで、集中型質量の場合は通常 [M] は対角行列となるが連続体からFEMにより離散化されたモデルの場合は動連成項も含まれる場合もあるので質量行列が対角行列にならない(コンシステントマスと呼ばれる)。ある節点がじっとしていても、もし隣の節点が加速度運動している場合、じっとしている節点にも慣性力が発生するということである。これは隣同士がもともと連続体としてつながっていたものを離散化したことにより生じる。(気軽に、節点がじっとしている・・などといったが、厳密には節点でなく、系の形状を一義的に定める変形パラメータ、つまり一般化座標のひとつがじっとしている、と言い変えなければならない。)
しかし、なお動連成項があるからというだけで、離散系という言葉が認められると言うには説得力が弱い。それにFEMで離散化されたものではなく、質点系を位置以外の別のパラメータで表せば動連成項もでてくる。
色々考えるとややこしくなるが、私にとって最も自然な見方は、数学的な扱いの明確な相違であるように思える。連続体は応力や歪といった空間的な微分の概念が用いられているが、離散系には、そういった概念は準備されていない。もしあったとしても(板の曲げ要素の節点パラメータ)形骸化したものでしかない。したがって、一般に連続体は時間・空間に関する偏微分方程式となり、離散系は、それより少し簡単な、時間に関する常微分方程式となる。
結局、FEMは連続体を近似的な離散系に置き換えるのであるが、数学的に言い直すと偏微分方程式を常微分方程式で近似表現する方法でもあるということになろうか。
まてまて、これで納得してしまうようでは、まだまだ修行が足りない。 GO TO 30
30 CONTINUE
以前のコラムでも述べたようにFEMの真髄は分布する応力を、その近傍の節点での静的に等価な合力に置き換えるところにある。それをさらに推し進めると、必ずしも「分布する応力」ではなく「もともと離散的に分布する力」を静的に等価な合力に置き換えても良いことに気づく。自由度の縮約である。
それについて述べた文献[2],[3] の説明は省略する。題名をみれば魂胆がおおよそ見えてくる。それと、離散系などと言う新しい言葉のお先棒を担いでいたのは実は他でもない・・・。
次は地球シミュレーターを用いての鉄筋コンクリート造超高層マンションの解析結果を紹介する予定。鉄筋(フープ筋なども全て)、杭、地盤も含めて丸ごとをモデル化している。
- [1] E.T.Whittaker, "Analytical Dynamics", Cambridge at the University Press, 3'd Edition, 1927
- [2] 橘英三郎、"離散化された密な構造モデルを粗なモデルに置き換える方法について",大阪大学大型計算機センター, 大次元行列研究会報文集, pp.48-57, 1972
- [3] 橘英三郎 "質点系における有限要素法について",JSSC,マトリックス構造解析法研究発表論文集,pp.21-26, 1975






