vol.35３体問題（Three-body problem）とGreenspanの心意気

男女の仲は３人が絡んだ３角関係になると話が厄介になる。谷崎潤一郎と、その妻千代、佐藤春夫　との不思議な三角関係は有名だ。谷崎は妻である千代を親友の佐藤に譲り渡したり、また取り戻そうとしたりでてんやわんや。

男女関係だけでない。物体の運動も同様である。引力のもとでの地球と太陽だけの運動については解ける。が、巨大隕石などがからむと３体問題となり解析的には特殊な例外を除いて一般解が得られない[1]。

本稿では、３体問題をGreenspan流[2]の差分形式で解く方法を紹介する。Greenspan 流とわざわざ「流」とつけたのには意味がある。通常、差分で解くと、エネルギー保存則などはあきらめてしまう。ところが、Greenspanはあきらめずに、エネルギー保存則が成立するようにちょっとした工夫をした。

まず、時間刻みを Δt とし Δt × ｋ 時間における i 質点の位置、速度、加速度をそれぞれベクトルX_i,k、 V_i,k、 A_i,k で表す。又、i 質点の質量をm_i とし、それに作用する力を F_i,k とする。位置、速度、加速度の差分表示を（1）、（2）式で表し、運動法則を (3) 式とする。

    (1)

    (2)

    (3)

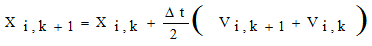
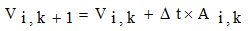
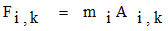
次に系になされる仕事 Ｗ を（4）式で定義する。

    (4)

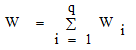
ただし　
ｑ　は質点の総数、　ｎは最終ステップ、　●は内積記号

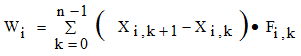
次に系のｋステップ目の運動エネルギーＫ_ｋを（5）式で、ポテンシャルエネルギーＵ_ｋを（6）式で定義する。

    (5)

ただし　

    (6)

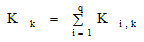
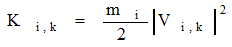
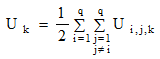
ただし　
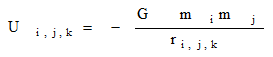
Ｇ　は重力定数で、

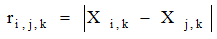
ここで、質点間の相互作用（引力）を次の (7)　式で与えると・・・

    (7)

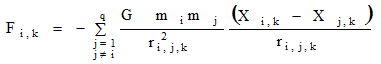
おっと、そうではなくGreenspanは （7）式のかわりに(8) 式を用いた。

    (8)

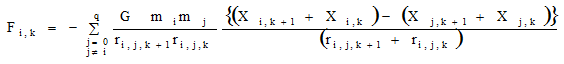
この工夫により、（4）式のＷiを媒介として、よく見慣れた保存則 (9) 式を導くことができる。（このプロセスは相当長くなるので省略する）

    (9)

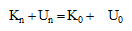
唐突に現れた(8) 式は何のことやら分かりにくいので次のように書き改めてみよう。

    (10)

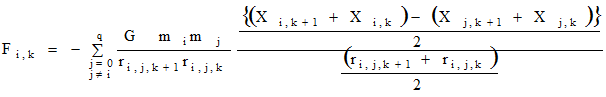
(7) 式と（10）式とを比べると（10）式ではk ステップ目と　k+1ステップ目の位置ベクトルが平等に扱われていることが分かる。言い換えると両者の位置の平均値が用いられている。そして何よりも特筆すべきは（10）式を用いることによりはじめて（9）式が成立する。何か（8）式はこじつけと感じるかもしれないが、差分を前提とした場合どちらに分があるとも言えない。

このようにGreenspanは、差分表現でも系全体に（9）式のような「エネルギー的な縛り」のできることを示した。勿論、（9）式は個々の質点の運動の精度を保証するものではない。精度には時間刻みの大きさやステップごとの収斂条件や切捨て誤差なども当然関係する。したがって、「エネルギー的な縛り」といっても、それは「系全体の柔らかな縛り」と言い換えるべきかもしれない。それでも、何の保証もないよりは少しはましではなかろうか。

この思想は、多体問題、熱伝導問題、流体問題などにも拡張されている。純粋理論と数値解析と分離したものとせず、両者の融合を狙っているようにも思えるので、敢えて文中の始めでは Greenspan流とした。

３体問題の簡単な例題を次に示す[3]。常数および初期条件として以下の値を設定している。

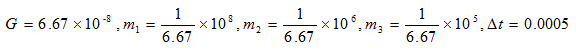
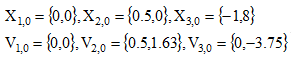
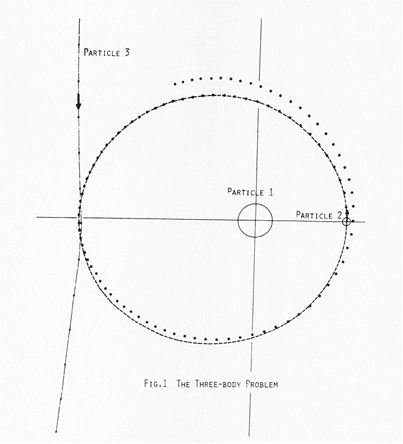
Particle１を固定とした場合のParticle２およびParticle３の軌跡を図１に示す。実線の円の軌跡はParticle３がない場合である。この結果については文献[3]よりそのまま転記しているがデータが一部散逸しているのであまり自信はない。チラッと眺める程度にしていただきたい。

差分を用いたから物理法則の成立はすべて「あきらめる」。そこで思考停止しなかったGreenspanの心意気に感心させられた。

なお、谷崎、千代、佐藤の３体問題？は、より複雑な多体問題であったことなどが瀬戸内寂聴尼ら多くの方々により詳細に語られていると聴く。

図１　３体問題の計算例