vol.36 関数空間（Function Space）、上下界定理とサン・ブナンの原理

ある殿さまが城の大広間の広さを自慢していた。家来にそこそこのお金を渡し、この広間を埋めつくすものを買い求めよ、と命じた。家来たちは安くてかさばる物、ムギ藁などをそれぞれ買ってきたが埋めつくすことができなかった。殿さまは大喜びだ。ところが一人の者が進み出て懐より１本のロウソクを取り出した。灯をともすと微かながらも薄暗い大広間の隅々まで光が満ちた。ロウソクの光は大広間の床どころかそれらを含む「空間」をも満たした、というお話。
「空間」などという言葉を聞くと、なぜかこの話を思い出す。長い間、工学の世界に身をおいてきた者から理学の世界を見ると、どうも工学は「その場しのぎ」で、理学は暗闇の中に１本のロウソクをともそうとしている高邁さを感じ・・・なくもない。
ところで、力学系では惑星間の運動のように「物と物との関係」でなく、空間（space）もしくは場（field）の問題ととらえたほうが大局的に分かり易い場合もある。
以下では、弾性解析における近似解の誤差について、抽象的な関数空間（Function Space）を用いて評価する方法を紹介したい。
材料の降伏条件でも知られているW.Pragerと相対性理論の専門家であるJ.L Syngeは関数空間をベースに弾性解析の近似解の誤差を幾何学的に証明した。ハイパーサークル法と呼ばれるものである[1,2]。
通常、応力解析では３つの基本条件がある。

• １）材料の応力と歪の関係　もしくは　構造材の力と変形の関係
• ２）応力もしくは力の釣合条件
• ３）歪の適合条件もしくは変形の連続条件

与えられた外力などに対して、この全てを満足する解が求まれば良いが、なかなか、そうは問屋がおろしてくれない。
有限要素法の普及していない時代は、工学では主に対象モデルの境界上における　２）、３）を如何に解決するかが問題であった。つまり境界値問題（boundary value problem）である[3]。しかし、実際には　２）や３）を少しゆるめたRitz 法などによる近似解で満足しなければならない場合も多かった[4]。ただ、しゃくなことに、正解が分からないので誤差が分からない[5]。これに答えたのが上記のハイパーサークル法だ。
一般的な境界値問題におけるRitz法のような近似解ではなく、その特殊な場合とも考えられる有限要素法で話を進めよう。（このアンダーラインの部分は後で再び引用する。）

• 画像拡大

  図-1　三角形要素の離散応力

• 画像拡大

  図-2　三角形要素の離散歪

「通常の」有限要素法では　２）の釣合条件を少しゆるめている。つまり隣り合った要素境界上での応力の釣合を諦めている。ただし、それらの境界上の不釣合応力は、静的等価な力に置き換えられて同じ境界上の節点（nodal point）での釣合で解消される。つまり、ほんのチョッと離れたところでの釣合で我慢している。いわゆる変形法系もしくは剛性法系の有限要素法だ。
又、今では人気がないが「通常でない」有限要素法では　３）の条件をゆるめる方法もある。こちらは応力法系の有限要素法となる。これには次の２つの煩わしい手続きが待っている。

【煩わしい手続き-１】

各要素に与えられる離散応力（変形法の節点力に対応）は、その要素の剛体的釣合条件を自動的に満足するように定義される。

【煩わしい手続き-２】

系全体から、不静定の離散応力を抽出する。

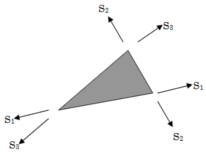
【煩わしい手続き-１】は、例えば３角形要素の場合、図-1のように３辺に沿って相反する向きの一対の力S₁、S₂、S₃を離散応力として採用する。

何？３辺に沿って相反する向き？　なにかピンとこない。 そー、慣れないものには抵抗感がともなうものだ。

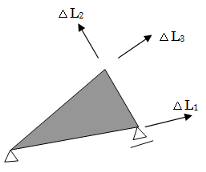
ここはぐっとこらえよう。これらS₁、S₂、S₃は３角形要素の剛体的釣合条件を自動的に満たす力となる。又、剛体的変位を差し引いたもので仕事量を介してS₁、S₂、S₃と対応する変位を離散歪とし図-2のように　△L₁、△L₂、△L₃で表す。

慣れないと言ったが、３角形要素でなく、もっと簡単なトラス材の場合は「軸力S₁」とそれに対応する伸縮量 △L₁となる。トラス材でも２次元なら変形法で両節点に２つずつ、計４つの節点力が与えられる。軸力S₁だけになるのは剛体的釣合条件から３つが消去されたと考えることができる。では、なぜこのように剛体的釣合条件を事前に処理しておくのだろうか？それはエネルギーの正定値性（positive definite）が要求されることによる。ひらたく言うと、S₁、S₂、S₃などは剛体的変形では仕事をしない。あるいはS₁、S₂、S₃などが△L₁、△L₂、△L₃などと1-1対応する。

【煩わしい手続き-２】は当初、コンピュータ解析での応力法系の最難関かと思われた。しかし古典的なJordan の消去法を用いることであっけなく解決されることがわかった[6]。

そして、これらの煩わしさにもかかわらず、1960年代から1970年代はじめまで変形法系よりもむしろ応力法系がJ.H.Argyrisらを中心としてヨーロッパで盛んに論じられた[7]。その理由の一つは、多少、手順が複雑でも未知数を少しでも減らしておきたいとの要求からであろう。（1960年代半ばからヨーロッパでは、超音速旅客機コンコルドの機体解析に追われることになる）
これら変形法系と応力法系の２系統の近似解が得られるようになり見直されたのがPrager とSyngeによる上下界定理である。
これは、変形分布を仮定し、部分的な釣合条件をゆるめた近似解の全歪エネルギーは正解のそれより小さく、応力分布を仮定し、部分的な変形の連続条件を満たさない近似解は正解のそれより大きいことを証明している(厳密には境界条件が関わるが省略する)。
この全歪エネルギーの上下界定理は境界値問題を扱う専門家にとっては魅力的なテーマであった。上下界論に言及した議論はその後も色々論じられているが[8,9,10] 基本的なところは明晰判然とせず結局は文献[1]に立ち返ることになる。

ところで、先に、一般的な境界値問題におけるRitz法のような近似解ではなく、その特殊な場合とも考えられる有限要素法で話を進めよう。と書いた。と言うのも当時はそうも解釈されていた。しかし、これは筆者の本意でない。有限要素法とRitz 法を結びつけるのは勝手だが、筆者は有限要素法はサン・ブナンの原理の区分的な採用だとシンプルに考えていた[11]。

そう断った上で・・・

• 画像拡大

  図-3　離散関数空間におけるhypercircle

• 画像拡大

  図-4　hyperircle の直径の最小化

弾性連続体をベースにしたPrager とSyngeによる関数空間にならい構造力学的な用語を一般的に定義して、離散系用の関数空間（離散関数空間）を組み立てた。この場合は、応力・歪を軸とする空間でなく、全ての離散応力S₁、S₂、S₃、・・（もしくは全ての離散歪 △L₁、△L₂、△L₃、・・）を軸とする関数空間での話となる。つまり離散系のあらゆる状態はこの空間内でのベクトルVで表されることになる。このベクトルのノルム 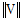を全ての要素についての離散応力と離散歪との積 (内積)　で定義する。

（材料が弾性で、外力が０のときV＝｛0｝とすれば、内積の公理やSchwartzの不等式は容易に証明される）
いま次の３種類のベクトルを考える。

V：１）、２）、３）の条件を満たす解（正解）
V^*：１）、２）の条件を満たす近似解（応力法系近似解）
V^"：１）、３）の条件を満たす近似解（変形法系近似解）

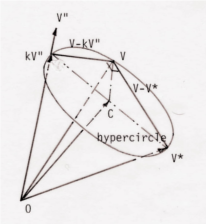
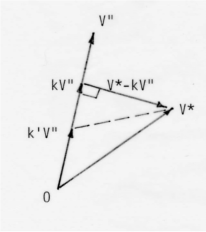
これらのベクトルは離散関数空間において図-3のような関係にあることが証明される。ここでk は任意の常数である。矛盾しているように聞こえるかもしれないが、上記二つの近似解を用いて、正解とのエネルギー誤差が正確に分かっている新たな近似解も得られる。V^* とｋV^"はhypercircle の直径の両端となり、その平均値　C　を新たな近似値とすると正解　V　とのエネルギー誤差が円の半径として正確に求められる。その誤差を小さくするには直径をできるだけ小さくすればよく、ｋV^"と　V^*-kV^"の直行条件よりｋが得られる（図-4）。

以下省略するがSyngeらが応力と歪をベースにした議論と同様、様々な上下界定理が幾何学的に証明できる。最後に、Synge らが導かなかったサン・ブナンの原理に関する上下界定理についてふれておく[12]。