vol.36 関数空間（Function Space）、上下界定理とサン・ブナンの原理

2015年07月28日

（2/2ページ）

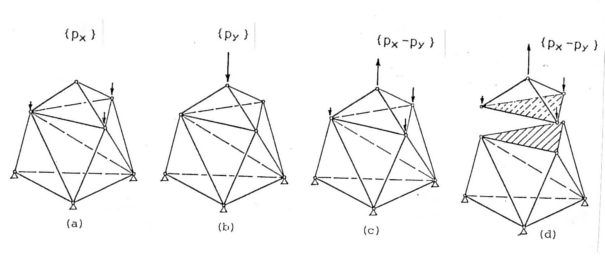
次の４種類のベクトルを考える。

V_ｘ：外力｛ｐ_ｘ｝が作用したときの正解　(a)図
V_ｙ：外力｛ｐ_ｘ｝と静的等価な外力｛ｐ_ｙ｝が作用したときの正解　(b)図
V_ｘｙ：外力｛ｐ_ｘ-ｐ_ｙ｝が作用したときの正解（V_ｘｙ＝V_ｘ-V_ｙ）　(c) 図
V_ｘｙ^* : 外力｛ｐ_ｘ-ｐ_ｙ｝が作用したとき　１）、２）の条件を満たす近似解　(d) 図

これらに対して次の不等式が成立する。

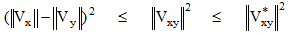
上下界ではさまれた項の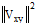は(c) 図に対応したもので合力が０の外力が作用した場合の変形エネルギーの２倍を意味している。この関係式は次の問題とむすびついている。

画像拡大
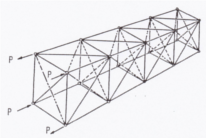
図-5　HoffによるSaint-Venant の原理の考察

N.J.Hoffは図-5に示すトラスの左端部に合力・合モーメントが０の力を加えた場合を計算し、それによる影響を調べた[13]。その結果、破線の部材がないと、右端部でも無視できない軸力の生じること、又、外殻に相当する部分の破線部を補強しても効果が無く、内部隔壁に相当する破線部が補強されることにより急速に影響が薄れていくことを示した。Y.C.FungはSaint-Venantの原理についての既往の研究を丁寧に紹介している[14]。（訳本に大いにお世話になった[15]。）ただしFungによるHoffへの評価は、従来の多くの考え方と整合していることの再確認にとどまっている。それはA.E.H.Loveにより次のように表現された Saint-Venant の原理[16]の証明に関する多くの議論との整合性である。

According to this principle, the strains that are produced in a body by the application, in a small part of its surface, of a system of forces statically equivalent to zero force and zero couple, are of negligible magnitude at distances which are large compared with the linear dimensions of the part.

しかしHoff の結論は整合性ではない。結論では、当時（1945年）簡略法でなされていたモノコックの機体解析をきちんとする必要性を説いていた。離散系においては静的等価な置き換えを安易にしてはならないことを示したものである。とは言え、手回し計算機では５０元程度の連立１次方程式を解くのが精一杯。電子計算機ENIACの誕生が1946年、さらに後退翼の解析を目的とした思われる有限要素法の発案が1956年である（本コラムVol.24、FEM のルーツと「たわみ角法」を参照）。このHoffの論文が構造解析の進展においてどの程度影響を与えたかは定かでない。

ところで、図-1、図-2　では「離散応力」「離散歪」なる用語を用いている。応力法系では確かにこれらに相当する概念は現れる。「離散応力」は剛体的釣合から独立したものであり、「離散歪」は剛体的変形では変化しない値である。しかし、どこかの文豪の猫ではないがきちんとした名前がない。そこで筆者は定義と名前付けを試みた。定義はすんなりといくがどうも名前付けがもう一つである。又、それらを基本に「離散体」と呼ぶモデルを組み立てた[17]。（本コラムのシリーズではそのモデルから得られた成果も多く含まれている。）

ちなみに、本稿での離散関数空間は、家元のJ.L.Synge先生がらのコメントをいただいている。本コラムVol.16（2009.11.12）「エネルギー誤差の分かっている近似解の話し」では、その抜粋を引用したが全文を付記しておく（写真-1）。

話をはじめに戻す。大広間に藁を並べていくように手堅く数値計算や実験を重ねていくか、一本のローソクを見つけようとするかは思案のしどころかもしれない。おっと、そんなことに拘らず、両方平行という手もありますよ。

写真-１　J.L.Synge 先生からの書簡 (31 March, 1977)

[1] W.Prager and J.L.Synge,"Approximations in Elasticity based on the Concept of Function Space", Quart. Appl. Math., Vol.V, No.3, 1947, pp.241-269
[2] J.L.Synge,"The Hypecircle in Mathematical Physics", Cambridge University Press, 1957
[3] これ以外に初期値問題（initial value problem）、固有値問題（Eigenvalue problem）があり有限要素法が普及するまでは物理学の応用面での重要テーマであった。例えば R.Courant und D.Hirbert,"Methoden der Mathematischen Physik", Zweiter Band, Springer, 1937, pp.473-544など。
[4] 倉西正嗣「弾性学」国際理工研究社（文献社による復刻版1970）, pp.101-102
[5] 誤差評価ではないが、試行級数を無限に増やしていくと正解に収れんするかなどは論じられている。参照：E.Trefftz,"Konvergenz und Fehlerschätzung beim Ritzschen Verfahren", Math., Ann.,100, 1928, pp.503-521
[6] J.S.シェムニスキー（山田嘉昭、川井忠彦　訳）「マトリックス構造解析の基礎理論」培風館、1971 のpp.184-210に詳しく述べられている。又、p.394 の上から10行目に「Jordan の方法は、つりあい方程式を用いて不静定力をきめるのに非常に有効であることがわかる。」とある。
[7] J.H.Argyris and S.Kelsey, "Energy Theorems and structural Analysis", Butterworths, 1960
[8] K.Washizu,"Bounds for Solutions of Boundary Value Problems", Faculty of Engineering, Univ. of Tokyo, 1952, pp.117-128
[9] B.M. Fraeijs de Veubeke, "Upper and Lower Bounds in Matrix Structural Analysis", Matrix Methods of Structural Analysis, Edited by B.M. Fraeijs de Veubeke, Pergamon Press, 1964, pp.165-201
[10] R.P.Shubinski and C.B.Brown,"Relationship of the Hypercircle Technique to the Energy Theorems", Journal of the Franklin Institute, Vol.298, No.1, 1974, pp.59-65
[11] 橘英三郎,"有限要素法とSaint-Venant の原理との関連性に関する一考察　－A Studv on the Relationships between Finite Element Method and Saint-Venant's Principle", JSSC,　第７回大会研究集会マトリクス構造解析法研究発表論文集, 1973, pp.11-18
[12] E.Tachibana, "Two Theorems on Saint-Venant's Principle in Discrete Structural Model", J. of Structural and Construction Engineering (Transactions of AIJ), No.351, 1985, pp.55-62
[13] N.J.Hoff. "The Applicability of Saint-Venant's Principle to Airplane Structures", J. Aero. Sci, 12, 1945, pp.455-460
[14] Y.C.Fung, "Foundation of Solid Mechanics", Prentice-Hall, 1965, p.300-309
[15] Y.C.ファン（大橋義夫、村上澄男、神谷紀生共訳）「固体の力学/理論」培風館, pp.306-316　なおp.308の（１）式左辺　UR' は　UR''の誤り（原本との確認により）
[16] A.E.H.Love, "A Treatise on the Mathematical Theory of Elasticity", Forth Edition, Cambridge at the University Press, 1934, p.132
[17] 最初の試みは、未完成であるが　橘英三郎,"一般座標の集まりよりなる離散体モデルの力学について（部分力の定義とその応用）",日本建築学会近畿支部研究報告集, 1976, pp.137-140　あたりから離散体という言葉を用いはじめている。多自由度系にいくつかのトポロジカルな概念を付与したモデルである。筆者の学位論文「構造力学における離散系の定式化に関する研究」1987年で一応完結している。本稿の内容はその第４章の一部を抜き出したものだ。上記文献[12]では査読での唐突な概念故の拒絶を怖れて敢えて離散関数空間の概念を用いていない。かなりドロクサイ証明となっている。