vol.34 行列(Matrix)とトポロジー(Topology)と鷲尾先生

2007年から2008年の間、横浜の地球シミュレータを利用して超高層ビルのシミュレーション解析を行った（本コラム2011年4月26日、Vol.22 地球シミュレーターとの出会い）。細い鉄筋の一本一本から杭や地盤にいたるまで、なるべく忠実にモデル化しての解析だ。それに到るにはかなり長い下地があったような気がする。その下地はこのあたりから始まる。

「ちょっと来てくれんか」との鷲尾先生から電話の声。（教授室と研究室とは５０ｍほど離れていた）又か・・・と思いながら部屋に入ると、
「何を勉強してるか知らんけど、下手な考え休むに似たり、や」
「それよりなー、最近ゴルフでスライスが多い。このアイアンの先の部分、マジックでしるしつけたところ、削ってもらいたいんやけどなー」
長年かけて出来上がった微妙な形状を勝手に変えて、と思いながらグラインダーで５分ぐらいで仕上げて渡すと、「あー、ありがとう」とにこにこ顔。
「ところで君、ポアンカレの３部作ぐらいは読んどるやろなー」
「いえ、読んでません」
「そーかー」

話はそれで終わった。
やがて柱梁接合部のせん断変形と剛域を考慮した骨組の解析コードを八幡製鉄と共同で開発を済ませ、次に有壁ラーメンの解析と実験にうつった。当時のコンピュータはメモリー容量が少なく苦労し、そのエッセンスを纏めてある会合で発表した（写真-１）

写真-1　Matrix構造解析法や有限要素法と同時進行の大次元行列問題

目次にあるような課題が40年以上たった今、解決されたかというとそうでもない。例えば、３次元立方体を10×10×10分割すれば1000個のソリッド要素となる。では、一桁上げて、100×100×100分割なら？
100万個のソリッド要素となり、節点に３自由度を与えると約300万元規模の問題となる。ウーン、頑張れば、なんとかなりそう。では、もう一桁上げて、1000×1000×1000分割なら？
それは無理。大体、そのようなムクのモデルはない。1000×1000×5　とか、もっと要領よくモデル化を、とか。結局４０年間で10分割レベルからせいぜい100分割レベルになったにすぎず目次のような課題は依然として残っている。

• 画像拡大

  図-1　開口部のある壁体のメッシュ分割図

• 画像拡大

  図-2　離散系の自由度の縮小

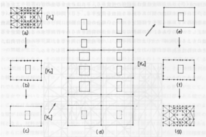
図-１は開口部のある壁体のFEMによるメッシュ分割図である。当時はこれでも直接解くのは相当苦しかった。

この一部（ユニット、Substructure、ブロックなどと呼ばれる）をとりだしたのが図-2の（a）図であり、その剛性行列を[K_a]とする。静的解析問題ならこの段階で内点は消去可能でありその縮小された剛性行列を（b）図の[K_b]とする。このように全てのユニットについて縮小した上で全体の剛性行列を組み立てて解く方法はユニット分割法やブロック消去法などと呼ばれる。

写真-1での「力学モデルにあらわれる密な離散系を疎な離散系に置換する方法について」は、これをさらに縮小しようとするのが目的だ。要は、（b）図の境界上に変形関数を仮定し、FEMと同様の方法で境界上の節点に生じる変形拘束力を静的に等価な４隅の節点力に振り分ける（Saint-Venantの原理）。これにより（c）図の[K_c]が得られる。このような前処理をした上で全体の剛性行列を組み立て（d）図の[K_d]を得る。後は荷重条件、境界条件を考慮して[K_d]の逆行列から（d)図の節点の変位を求め、逆の手順で（e）、（f）、（g）と順に解凍して近似解を得る。

格子型、連層型の耐震壁モデルを対象にして実験結果および近似式を用いない解との比較を行っているが、それは文献[2]にゆずる。

少し話しを後にもどすと1960年代後半から構造解析の分野では「マトリックス法」という言葉が盛んに用いられはじめた。そして、鷲尾先生は鋼構造協会（JSSC）などの場で「どうもその呼び名が気にいらん。微分を使ったら微分法か」と笑いながら噛みついていた。JSSCの重鎮でもあり、日本建築学会の副会長もされてはいたが我が師ながら当時院生だった私は何となく恥ずかしい気がしていた。ぼちぼち老境に入ったか。なにしろ、フォームを直さず、アイアンを削るんだから。それに比べ、鷲津先生や川井先生や吉識先生は光ってるなー。そう思っていた。

しかし、マトリックス法にかみついたのは単なる言いがかりではなかった。鷲尾先生は「行列」の概念にいち早く着目し、1934年頃から「行列」を用いた構造解析に関する論文を発表している[3,4,5]。そして、その源流は1926前後に量子力学の表現法に関してハイゼンベルグやマックス・ボルンを中心として演算子をまとめて表象した「行列力学」までつながっていく。ただし「つながる」という意味は「行列」により簡潔に表現したりシステマティクな数式処理ができるという意味であり、それはマックス・ボルンがハイゼンベルグの複雑な数式を見てのアドバイスでもあった。コンピュータのなかった時代であり、ＤＯループを前提としたマトリックス構造解析法とは力点の置き所が異なるのは当然であろう。最近では「行列力学」の呼称は消えつつあるので、やはり呼称は内容の本質に近いものが残るのかもしれない。