vol.33 スナップスルー(Snap-Through)と非線形計画法(nonlinear programming)
−話せば長いことながら入り口だけでも−

以前にもふれたが（Vol.18, 曲がってもいいじゃないか）３年終了時点で単位が大分足りない学生がいた。

「卒論と卒業設計ができても単位不足で卒業できないかも知れない。４年では少し多めに単位をとるように」と言った。その学生が卒業のときに「先生のおかげで４単位も多くとった」と口をとがらせた。
４単位分だけアルバイトの時間が減ったという。人それぞれの事情がある。

私のようなうっかり者にとっては有難いアドバイスも、絶妙のコントロールで日々過ごしている者にとってはよけいなお節介だった。大学は小学校ではない。立派に自己責任のとれる人の集まりだ。
そして、天体も、この学生と同様に絶妙のコントロールで運行している、と言えなくもない[1]。

しかし天体はすこし大袈裟なので図１のトラスをとりあげる。それも静的な問題に限定しよう。このトラスは体育館をイメージしてもよい。山型の屋根をもち、そのハラミダシをおさえる両側の柱を右側の２本の柱で代表している。

このトラスの節点1に強制変位Δを下向きに与えた場合、節点１の反力Rについて考えよう。
未知変位は節点1の水平変位と節点2の水平および鉛直変位であり、自由度は３となる。
それらを便宜上X(1),　X(2),　X(3)で表すことにする。材料は弾性Eとし、断面積はすべてAとしよう。

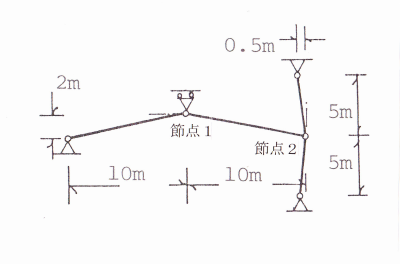
図１　簡単なトラス構造 [2]

「なーんだ、簡単な問題だ」

が・・・これがなかなかの難物である。
図２が解析結果であり節点１の反力Rと強制変位Δの関係を表しているのが「実線」である[2]。
（とりあえずは実線以外は無視）　「エー、何これ？」

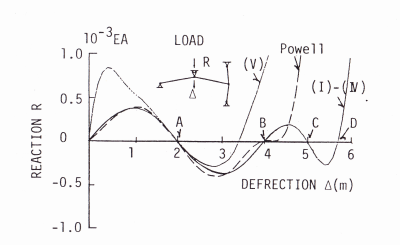
図２　反力Rと強制変位Δとの関係 [2]

まーまー、落ち着いて。おおまかな話の流れは次のようになる。

１）節点１の下向きの強制変位Δが１ｍ過ぎるあたりから屋根の勾配がゆるくなるので、反力Rは下がりはじめる。やがて、Δが２ｍになると屋根は水平になり反力Rは０となる。（図２では点A）
２）さらに強制変位Δを増やすと反力は負に変じる。つまり節点１は下に引張られるわけだ。Δが４ｍになるとちょうど上下対称の位置にくるので、反力Rは再び０となる（図２では点B)。
３）さらに強制変位を増やすと、こんどは節点２が内側（左側）に引張られはじめる。やがて２本の柱が一直線になったとき水平抵抗は０となり反力Rも０となる。（図２では点C)　その後しばらく反力Rは負となる。
４）節点２が結果的に０.５ｍだけ左に移動したとき（図２では点D)、再び反力Rは０となり、それ以降は上昇しつづける。
（＊注　点Cや点Dの正確な位置は実際に解析しないとわからない）