
- 株式会社JSOL エンジニアリング事業本部 技術顧問
- 広島大学名誉教授、株式会社CEM研究所代表取締役
私は上森武君(当時は広島大学大学院博士課程の学生、現在は岡山大学准教授)と一緒に大ひずみ繰返し塑性モデルのYoshida-Uemori (Y-U) model1)-3)を2002~2003年に発表し、その後もいくつかの改良をしています。幸いなことに、Y-U modelはJSTAMPをはじめ、ほとんどの市販の板材成形シミュレーションソフトに採用され、とくに高張力鋼板のスプリングバック計算にはこのモデルが不可欠という評価を得るまでになっています。
今回以降は、Y-U modelについて、モデルの枠組みと特徴、モデル開発にあたってのポイントなどをお話しさせていただこうと思います。ただ、このモデルの枠組みを理解するためには、塑性理論の概要とともに繰返し塑性理論(cyclic plasticity)の歴史的発展をざっと知っておいていただいたほうがいいと思います。ということで、今回は塑性理論の枠組みを簡単に解説します。
1.降伏条件・降伏関数・降伏曲面について
塑性構成式(応力とひずみの関係式のことです)の話では、降伏条件(yield criterion)、降伏関数(yield function)、降伏曲面(yield surfaceまたはyield locus)という言葉が多く出てきます。降伏とは材料が弾性変形のみの状態から塑性変形を開始する条件です。例えば板を一方向に単純に引張ったり圧縮したときを考えると、そのときの応力σが材料の降伏強さ(または降伏応力)Yに到達したときに降伏を開始するので、このときの降伏条件は以下のように表されます。
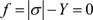
板材成形などでは、一方向の単純な応力だけでなく、x(板の圧延方向), y(圧延直交方向)の二方向の応力成分(\(\sigma_{ xx }\),\(\sigma_{ yy }\),\(\tau_{ xy }\))が組み合わさって作用するのが普通です。このときの降伏条件は、一般的に次式で表されます。
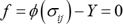
ここで、\(\phi(\sigma_{ij})\) は降伏関数といいます。例えば最も広く使われているミーゼス(von Mises)の降伏条件は以下のように表されます。
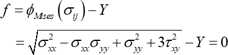
なお、3次元の応力が作用する場合には、以下のようになります。
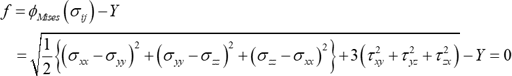
ここで、\(\phi(\sigma_{ij})\) は降伏関数といいます。なお、トレスカ(Tresca)は最大せん断応力によって降伏が起こるとして、材料に作用する最大主応力 \(\sigma_{ max }\) と最小主応力 \(\sigma_{ min }\) を用いて、以下の降伏条件を提案しています。
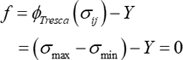
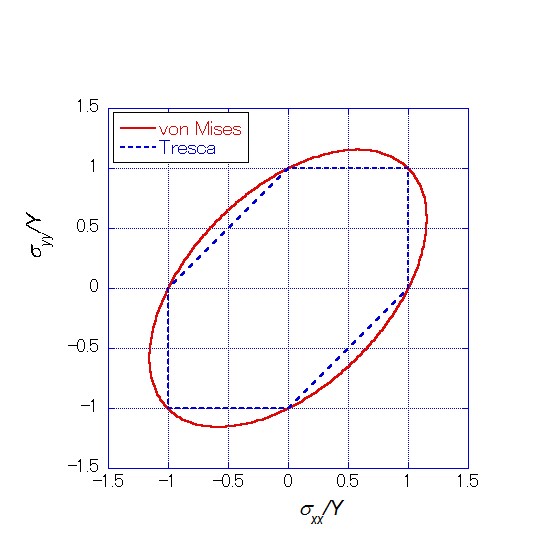
降伏条件を応力空間(または平面)に図示すると、これは閉曲面として表せるので、これを降伏曲面(yield surfaceまたはyield locus)と呼びます。たとえば、von Mises式(2)で、せん断応力成分 \(\tau_{ xy }\) = 0 の場合の降伏曲面 \(f\) は、Fig. 1 に示すように、(\(\sigma_{ xx }\),\(\sigma_{ yy }\)) 応力平面上で45°傾いた楕円形、Tresca式(5)ではそれに内接した六角形となります。多くの金属材料が von Mises と Tresca の条件の間で降伏することがわかっています。応力点が降伏曲面の中にある場合(応力状態 \(f \lt\) 0 )には弾性応力-ひずみ応答となり、降伏曲面の中にある場合(応力状態 \(f\) = 0 )には材料は降伏して弾塑性応力-ひずみ応答となります。このように、降伏曲面は材料が塑性変形中であるかどうか(弾/塑性判別)を示す重要な役割を果たしています。なお、降伏曲面は応力空間中で必ず外向きに凸である(凸面性、convexity)ことが必要です。
ここで、塑性力学でよく使われる偏差応力(deviatoric stress)について簡単に説明しておきます。金属材料に垂直応力が等方的に作用する場合(\(\sigma_{ xx }\)=\(\sigma_{ yy }\)=\(\sigma_{ zz }\))には塑性変形は起こりません。例えば、深い海の底に金属材料を沈めても高い水圧 \(p\)(\(\sigma_{ xx }\)=\(\sigma_{ yy }\)=\(\sigma_{ zz }\)=\(-p\))で材料が降伏することはありません。そこで、垂直応力三成分の平均値(平均応力といいます):
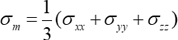
を垂直応力成分 \(\sigma_{ xx }\),\(\sigma_{ yy }\),\(\sigma_{ zz }\) から差し引いて、偏差応力 \(s_{ij}\) を次式で定義します。
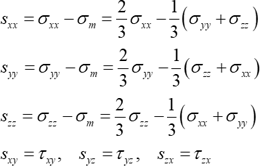
Von Mises の降伏条件を偏差応力で書くと次のようになります。

2.加工硬化則
2.1 単軸引張り(または圧縮)における加工硬化
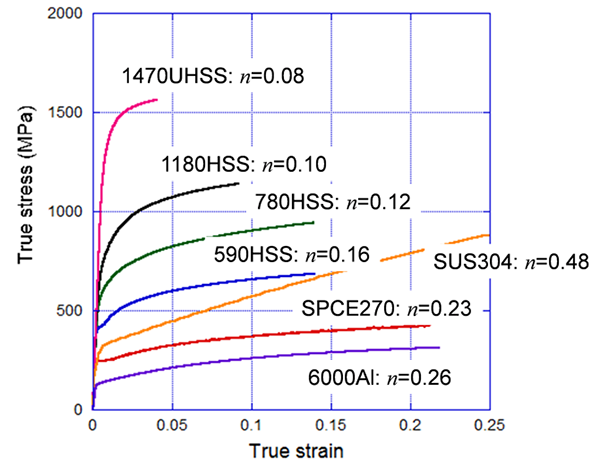
種々の材料の単軸引張り試験から得られた応力-ひずみ曲線を Fig. 2 に示します。これを見ると、材料の塑性変形に要する応力(流動応力または変形抵抗ともいう)は材料ごとに大きく違うが、同時に加工硬化(ひずみの増大に伴う流動応力の増加のことで、ひずみ硬化ともいう)も材料ごとに大きく異なっていることがわかります。
ひずみ \(\varepsilon\) は弾性ひずみ \(\varepsilon^{e}\) と塑性ひずみ \(\varepsilon^{p}\) に分けられます。
(\(\sigma=C(\varepsilon^{p})^{n}\))
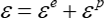
単軸引張りまたは圧縮の場合には、材料の加工硬化は塑性ひずみ \(\begin{vmatrix}\varepsilon^{ p }\end{vmatrix}\) の増加とともに材料の応力(流動応力、変形抵抗ともいう)が大きくなるので、これは次のように表されます。
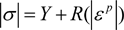
ここで、\(Y\) は材料の初期降伏応力で、\(R(\begin{vmatrix}\varepsilon^{ p }\end{vmatrix})\) は加工硬化応力です。以下にいくつかの加工硬化モデルを示します。
(線形硬化モデル:Fig. 2(a))
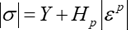
(Voceモデル:Fig. 2(b))
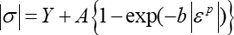
(Ludwikモデル:Fig. 2(c))

(Swiftモデル:Fig. 2(d))
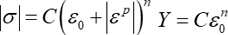
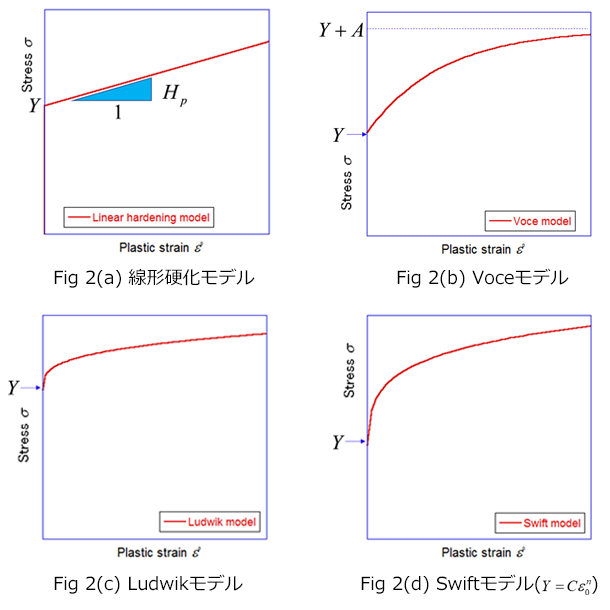
なお、Ludwikモデルにおいて\(Y=0\)、あるいはSwiftモデルにおいて、\(\varepsilon_{0}=0\)の場合には
(n乗硬化モデル)
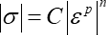
となり、このときの n は加工硬化指数あるいは n値と呼ばれます。Fig. 2 中に記載のように、加工硬化が大きい材料ほど n値が大きくなります。
2.2 多軸応力における加工硬化(等方硬化則)
次に、多軸応力状態における加工硬化は、相当応力 \(\bar{\sigma}\) と相当塑性ひずみ \(\bar{\varepsilon}\) を使って、次のように表します。
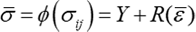
この式でわかるように、相当応力 \(\bar{\sigma}\) は降伏関数 \(\phi(\sigma_{ij})\geq0\) で計算される応力値そのものです。相当塑性ひずみ \(\bar{\varepsilon}\geq0\) は、その増分(微小変化量) \(d\bar{\varepsilon}\geq0\) が、塑性仕事等価を仮定して、次のように定義されます。
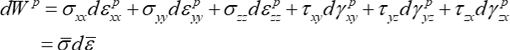
すなわち、塑性仕事増分:\(dW^{p}\)=相当応力:\(\bar{\sigma}\)×相当塑性ひずみ増分:\(d\bar{\varepsilon}\)によって相当塑性ひずみ増分が定義されます。Von Misesの降伏関数(相当応力)を使うと、\(d\bar{\varepsilon}\)は次式のようになります。
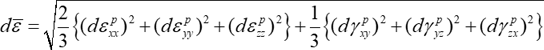
この式の誘導には塑性構成式を使う必要がありますが、詳細は引用文献 4) を参照してください。相当塑性ひずみはその増分 \(d\bar{\varepsilon}\) を累積したものです。すなわち、
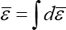
加工硬化式(16)は、Fig. 3 に模式的に示すように、降伏曲面の大きさが初期に \(Y\) であったものが、塑性変形とともに \(Y+R(\bar{\varepsilon})\) に拡大していることを示します。このように、降伏曲面の中心が固定したまま、その形を変えずに、塑性変形とともに拡大してゆくので、この硬化モデルは等方硬化(isotropic hardening)モデル(または等方硬化則)といいます。なお、塑性変形後の降伏曲面は後続降伏曲面(subsequent yield surface)と呼びます。論文などでは「等塑性仕事曲面」という言葉が時々でてきますが、これは「等方硬化モデルを仮定したときの後続降伏曲面」を指しています。
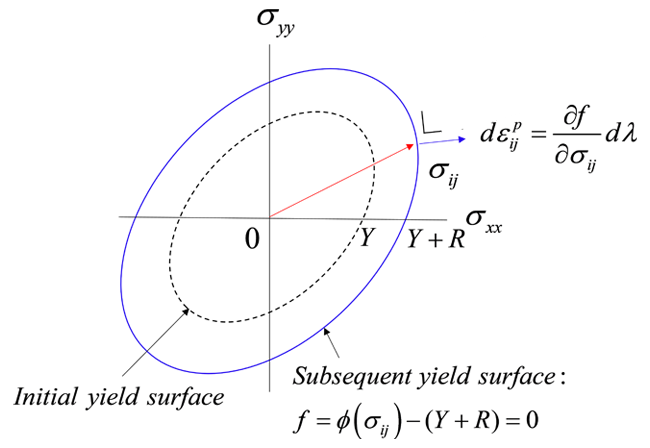
塑性変形が継続しているときには、応力点は必ずその時点の後続降伏曲面上に存在することには注意が必要です。速度非依存の塑性モデルでは、応力点は降伏曲面の内側( \(f\lt0\):弾性応力-ひずみ応答)か曲面上( \(f=0\):塑性応答)にしかなく、降伏曲面の外側には存在しません。
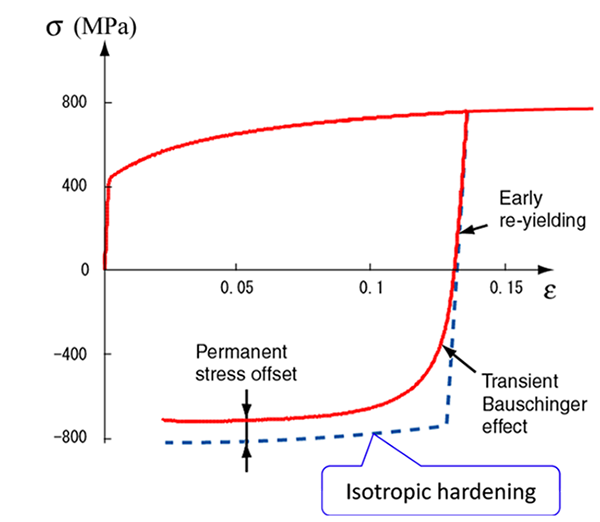
なお、等方硬化モデルでは応力反転に伴うバウシンガー効果(応力反転時に流動応力が低下する現象)は表現できません(Fig. 4参照)。バウシンガー効果を表すには、降伏曲面の中心が移動する移動硬化(kinematic hardening)モデルを使うのが最も一般的ですが、これについては後述します。
3.関連流動則
塑性構成式には、「塑性ひずみ増分 \(d\varepsilon^{p}_{ij}\) の方向は、応力点の存在する降伏曲面の垂直方向に一致する(垂直則と言います。Fig. 3 参照)」とする塑性ポテンシャル理論が使われます。この理論については引用文献 4) を参照していただきたいが、これは次式で表現されます。
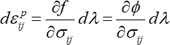
ここで、\(d\lambda=d\varepsilon\geq0\) となります。このように、降伏曲面に対する垂直則によって決められる塑性ひずみ増分の決定は関連流動則と呼ばれます。例えば Von Mises の降伏関数式(3)を用いると、関連流動則式(20)より塑性構成式は以下のようになります。
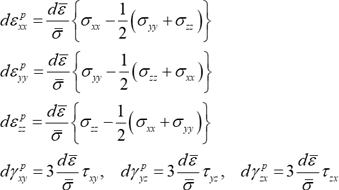
これを偏差応力を用いて表現すると次のようになります。
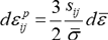
このように、降伏曲面は塑性ひずみ増分の進行方向を決定するという重要な役割を持ちます。
4.移動硬化モデルによるバウシンガー効果の表現
バウシンガー効果の応力—ひずみ応答は、塑性変形に伴う降伏曲面の移動によって表現できます。塑性変形後の降伏曲面の中心を \(\alpha_{ij}\) (背応力:backstress といいます)と書くと、塑性変形後の降伏条件(後続降伏条件)は次式で表現できます (Fig. 5参照)。
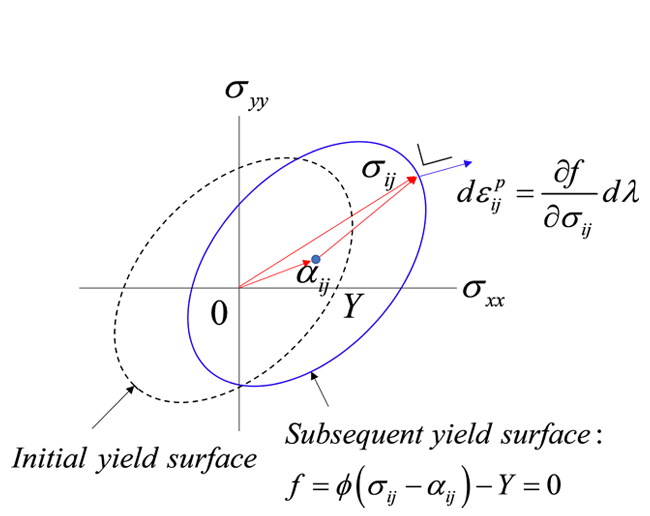

ここで、降伏曲面の形状と大きさは塑性変形によって変化しないとしています。この塑性モデルは移動硬化(kinematic hardening)モデルと呼ばれます。このモデルで重要なのは、降伏曲面の中心を \(\alpha_{ij}\) が塑性変形によってどのように変化するか(これを移動硬化則といいます)です。
移動硬化モデルのアイデアを一番初めに提案したプラガー(Prager5), 1955)は、次式で示す線形移動硬化則を仮定しました。
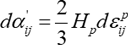
ここで、\(d\alpha_{ij}\)は偏差背応力で、 \(H_{p}\) は加工硬化率(一定値)です。単軸応力状態では、式(24)は次のようになります。
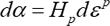
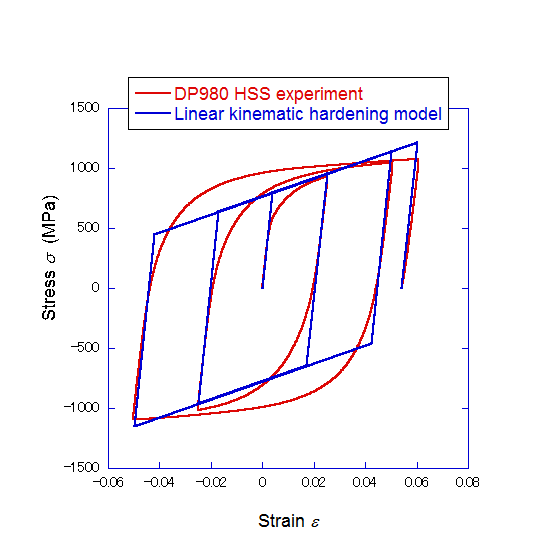
このモデルを用いて繰返し弾塑性変形における応力-ひずみ応答を計算した例をDP980高張力鋼鈑の実験結果と比較したものを Fig. 6 に示します。モデルによる計算結果はバウシンガー効果を定性的には表現していますが、線形硬化の仮定が現実とは大きく異なっているため、最近ではこのモデルはほとんど使われていません(私の記憶では、1980~1990年代初め頃までは等方硬化と組合わせて構造強度計算などには使われていました)。
移動硬化モデルのその後の発展は、どのようにしてバウシンガー効果を含む非線形応力-ひずみ応答を表現するかということに注力されることになります。次回ではいくつかの代表的な非線形移動硬化モデルについてお話ししたいと思います。
- Yoshida, F., Uemori, T., Fujiwara, K., Elastic-plastic behavior of steel sheets under in-plane cyclic tension-compression at large strain. International Journal of Plasticity 18, (2002), pp.633-659.
- Yoshida, F., Uemori, T., A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation. International Journal of Plasticity 18, (2002), pp.661-686.
- Yoshida, F., Uemori, T., 2003. A model of large-strain cyclic plasticity and its application to springback simulation. International. Journal of Mechanical Sciences 45, (2003), pp.1687-1702.
- 吉田総仁,弾塑性力学の基礎,(1997),第9~10章,共立出版,ISBN4-320-08114-5
- Prager, W., The theory of plasticity: a survey of recent achievements (James Clayton Lecture), Proceedings of Institute of Mechanical Engineering, 169 (1955), pp.41-57
- ※ 記載されている製品およびサービスの名称は、それぞれの所有者の商標または登録商標です。
技術ブログカテゴリ
新着記事
- 分子シミュレーションで設計するプラスチックリサイクル
- 形状設計フェーズでの組み立て精度向上によるコスト削減
~ 組み立てCE検討ツールのご紹介 ~ - JSOLが考える「溶接シミュレーションと工場デジタルツインが実現する工程設計」について講演しました
- リアルワールドの自動車衝突安全に向けて
- 機械学習で加速する材料シミュレーション技術
- ノウハウ不要!樹脂の複雑な材料特性を簡単にフィッティング 〜 材料同定ツールと高精度ユーザーサブルーチンの活用事例 〜
- 樹脂材やゴム材の高精度予測に向けたパラメータ同定
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(後編)
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(前編)
- 製造業におけるマテリアルズ・インフォマティクス
