
- 株式会社JSOL エンジニアリング事業本部 技術顧問
- 広島大学名誉教授、株式会社CEM研究所代表取締役
1.はじめに
先回のコラム記事では塑性力学(材料モデル)の基礎についてお話ししました。その中で、降伏曲面が塑性変形とともに大きくなる等方硬化モデルと降伏曲面が移動する移動硬化モデルの概念について述べました。移動硬化の最も簡単なモデルである線形移動硬化モデルについてもふれています。今回は、バウシンガー効果の応力-ひずみ曲線をもっと現実に近い形で表現する非線形移動硬化モデルについて、いくつかの代表的な例を示します。
2.いくつかの非線形移動硬化モデル
移動硬化モデルについて簡単に復習します。塑性変形後の降伏曲面 \(f\) の中心を \(\alpha_{ij}\)(背応力:backstress)と書くと、塑性変形後の降伏条件(後続降伏条件)は次式で表現できます(Fig. 1参照)。
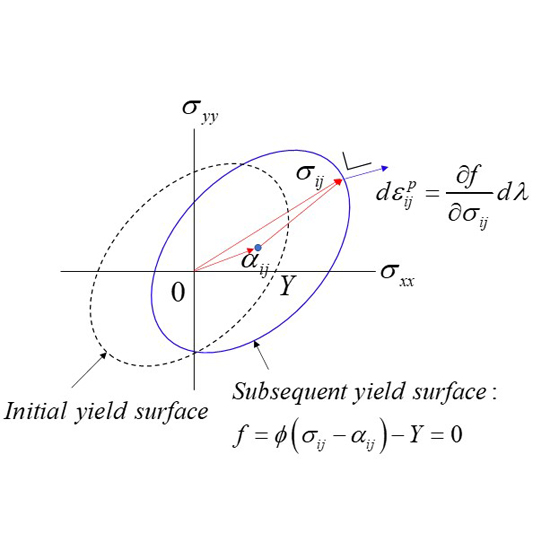
\[f=\phi(\sigma_{ij}-\alpha_{ij})-Y=0\]
ここで、降伏曲面の形状と大きさは塑性変形によって変化しません。移動硬化(kinematic hardening)モデルとは、降伏曲面の中心\(\alpha_{ij}\)が塑性変形によってどのように変化するかの定式化です。
2.1 Armstrong-Frederickモデル
非線形移動硬化モデルの代表的なものにArmstrong-Frederick(A-F)モデル1)(1967)があります。これは次式で表現されます。
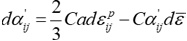
ここで、\(\alpha'_{ij}\),\(d\alpha'_{ij}\)は背応力(backstress)の偏差成分とその増分です。すなわち
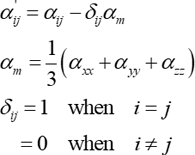
式(2)で、\(d\varepsilon^{p}_{ij}\) ,\(d\bar{\varepsilon}\) はそれぞれ塑性ひずみ増分、相当塑性ひずみ増分、\(a, C\) は材料定数です。これを通常の応力成分で書くと次のようになります。
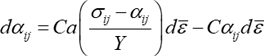
単軸応力状態では次のようになります。
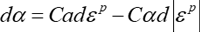
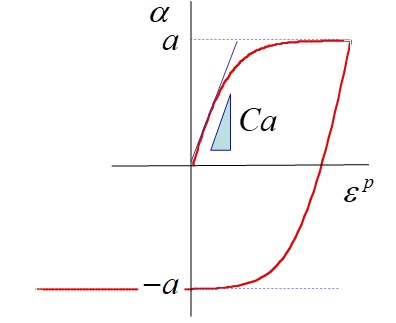
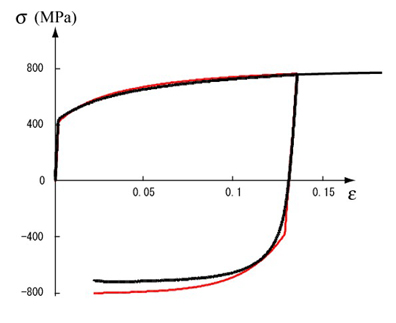
この右辺の第一項は線形移動硬化(背応力増分 \(d\alpha\) が塑性ひずみ増分 \(d\varepsilon^{p}\) の線形関数)の形になっていますが、第二項(これは動的回復項と呼ばれることがあります)があるため、塑性ひずみの進行とともに移動硬化の進行速度が遅く(すなわち硬化係数が小さく)なります(Fig. 2参照)。Fig. 3には、一例として、590MPa高張力鋼板の引張り・圧縮の応力-ひずみ関係を等方硬化+A-F移動硬化モデルを用いて計算した結果を示します。バウシンガー効果による非線形な応力—ひずみ応答が表現できています。ただ、応力反転の計算結果と実験結果には少しずれがあることもわかります。
2.2 Chabocheモデル
Chaboche-Rousselier2)(1983)はA-Fモデルの背応力成分を多数足し合わせることにより、さらに実際の非線形応力—ひずみ応答に近い再現ができるようにしました。すなわち、
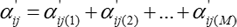
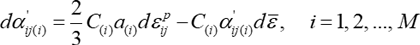
Chabocheモデルは非線形移動硬化モデルの代表的なものとして有名ですが、そのもととなった A-F モデル (1967)はChabocheらの論文(1983)によって、発表から16年後に一躍脚光を浴びることになりました。というのは、Armstrong-Frederickの論文は学会誌ではなく、彼らが所属していたBerkley原子力研究所の所内研究報告集に掲載されていたので、Chabocheらがその発展形の論文を発表するまではほとんど知られていなかったからです。Chabocheモデルは表現力に優れていますが、A-F 移動硬化項が1個増えるごとに、1個のテンソル変数 \(\alpha_{ij(i)}\)(6成分)と2個の材料パラメータ \(C_{(i)},\alpha_{(i)}\) が増えてゆきますので、計算負荷の点からあまり多くの項数を使うのは現実的ではありません。なお、Chabocheモデルは、式(7)で与えられる移動硬化と降伏曲面が拡大する等方硬化の組合せ(式(8)参照)として提案されています。
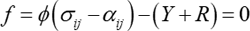
ここで、Rは等方硬化応力で、Chabocheらはこれを次式で示すVoce型を仮定しています。
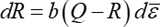
すなわち
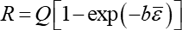
2.3 Dafalias-Popovの二曲面モデル
Dafalias-Popov3)(1975)は降伏曲面の移動範囲を表す境界曲面(bounding surface)を用いた二曲面モデルを提案しました。その概念を単軸引張り・圧縮における応力と塑性ひずみ模式図(Fig. 4)を用いて説明します。単軸引張りの応力-塑性ひずみ応答は直線 AA' に漸近し、応力反転ではこれは BB' に漸近するとします。 AA',BB' の傾きすなわち収束する塑性硬化係数を \(d\sigma | d\varepsilon^{p}=H^{p}_{0}\) と書きます。この AA',BB' は降伏曲面の移動する範囲(境界)を表しています。 AA',BB' の境界間距離を \(2B\) と書きます。Fig. 4を参照して、塑性硬化係数\(d\sigma | d\varepsilon^{p}=H^{p}\)を次式のように表します。
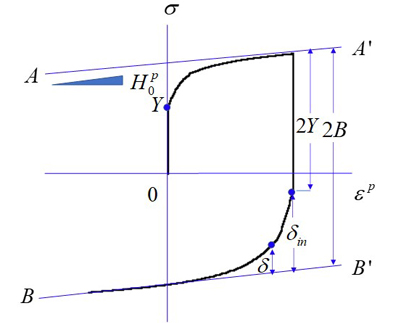
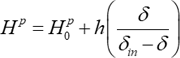
ここで、\(\delta\) は現在の応力点と境界点の距離で、 \(\delta_{in} = 2(B-Y)\) は降伏曲面の移動できる最大値を表し、\(h\) は \(\delta_{in}\) の関数(境界の大きさ \(B\) が変化しなければ、\(h\) は一定値)です。
このモデルを多軸応力状態に拡張したものをFig. 5に示します。降伏曲面 \(f\)(大きさ \(Y\),中心 \(\alpha_{ij}\) )は境界曲面 \(F\)(大きさ \(B\),中心 \(\beta_{ij}\) )の中を移動しますが、そのときの塑性硬化係数は式(11)で与えられますが、 \(\delta\) は、Fig. 5に示すように、降伏曲面上の応力点 \(\sigma_{ij}\) と対応する境界曲面上の応力点 \(\sigma^{*}_{ij}\) の距離で定義しています。すなわち、
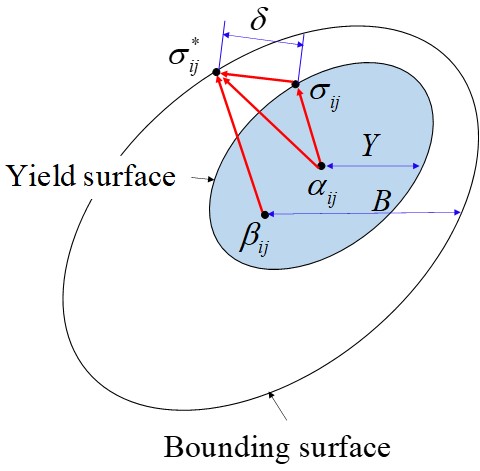
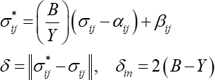
なお、境界曲面については、移動硬化のみならず等方硬化も組合わせることができます。このモデルは比較的簡単ですが、実際には材料ごとに異なるバウシンガー効果の応力-ひずみ曲線の形状が、式(11)で与えられるため、同じ形になってしまうという欠点があります。
2.4 Mrózの多曲面モデル
Mróz4)(1967)は各曲面 \(f_{(k)}\)\((k = 1, 2, …, M)\)が固有の塑性硬化係数を持つ多曲面モデルを提案しました(Fig. 6参照)。多曲面の内、一番内側にあるのが降伏曲面になります。降伏曲面が移動するとともに、外側の曲面に次々と接触し、これらの曲面は降伏曲面と一緒に移動します。降伏曲面と接している一番外側の曲面の持つ硬化係数が応力-ひずみ計算に採用されます。各曲面の移動硬化則は次式で与えられます。
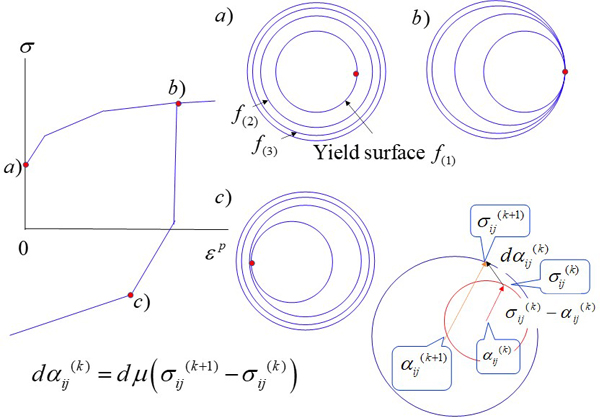
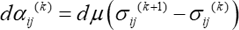
このモデルはA-Fモデルとともに早い段階で提案された非線形移動硬化モデルで、独創的なものです。ただ、このモデルも多くの曲面の中心 \(\alpha^{(k)}_{ij}\)(各6成分)が状態変数となり、曲面の数も通常は4個以上必要となり、計算コストという面からは欠点があります。
余談になりますが、私は、大学の卒論研究でこの論文を読んで、その洗練した内容に感動し、繰返し塑性問題に興味を持ちました。Mróz先生にはワルシャワの基礎工学研究所に呼んでいただき、半月ほど滞在させていただいたこともあり、大変お世話にもなりました。
3.おわりに
今回は、いくつかの代表的な非線形移動硬化モデルを紹介させていただきました。この他にも、ラチェット現象の記述のためのOhno-Wang5)(OW)モデル(1993)、D-Pモデルを基礎としたHassan-Kyriakidesモデル6)(1992)、さらに移動硬化を使わずに降伏曲面のゆがみでバウシンガー効果を表現するBarlatらのモデル7)(2011)など多数あります。次回は、私たちのYoshida-Uemori(Y-U,2002-2003)モデルについて、その開発の経緯も含めて、解説したいと思います。
- Armstrong, P. J., Frederick, C. O., 1966. A mathematical representation of the multiaxial Bauschinger effect. GEGB report RD/B/N731. Berkley Nuclear Laboratories.
- Chaboche, J.L., Rousselier, G., 1983. On the plastic and viscoplastic constitutive equations, part I and II., ASME Journal of Pressure Vessel Technology, 105, 153-164.
- Dafalias, Y. F., Popov, E. P., 1975.A model of nonliniearly hardening materials for complex loading. Acta Mecanica 21, 173-192.
- Mróz, Z., 1967. On the description of anisotropic work hardening. J. Mech. Phys. Solids 15, 163-175.
- Ohno N, Wang J-D, 1993. Nonlinear kinematic hardening rule with critical state of dynamic recovery, Part I: Formulation and basic features for ratchetting behavior, Int. J. Plasticity 9, 375-390.
- Hassan T., Kyriakides S., 1992. Ratcheting in cyclic plasticity, Part I: Uniaxial behavior, Int. J. Plasticity 8, 91-116.
- Barlat, F., Gracio, J. J., Rauch, E. F., Vincze, G., 2011. An alternative to kinematic hardening in classical plasticity, Int. J. Plasticity 27, 1309-1327.
- ※ 記載されている製品およびサービスの名称は、それぞれの所有者の商標または登録商標です。
技術ブログカテゴリ
新着記事
- 分子シミュレーションで設計するプラスチックリサイクル
- 形状設計フェーズでの組み立て精度向上によるコスト削減
~ 組み立てCE検討ツールのご紹介 ~ - JSOLが考える「溶接シミュレーションと工場デジタルツインが実現する工程設計」について講演しました
- リアルワールドの自動車衝突安全に向けて
- 機械学習で加速する材料シミュレーション技術
- ノウハウ不要!樹脂の複雑な材料特性を簡単にフィッティング 〜 材料同定ツールと高精度ユーザーサブルーチンの活用事例 〜
- 樹脂材やゴム材の高精度予測に向けたパラメータ同定
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(後編)
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(前編)
- 製造業におけるマテリアルズ・インフォマティクス
