
- 株式会社JSOL エンジニアリング事業本部 技術顧問
- 広島大学名誉教授、株式会社CEM研究所代表取締役
1.はじめに
今回からはYoshida-Uemori (Y-U) model1)-3)について、その開発の動機やモデル化のポイントについてお話しをしたいと思います。Y-U modelに関する論文は2001-2002年にかけて、International Journal of Plasticity1),2)とInternational Journal of Mechanical Sciences3)(いずれもElsevier出版社)に投稿し、2002-2003年に掲載されています。ですから、この研究に本格的に着手したのは2000年頃です。当時の研究ノートを見ると、1990年代後半には従来モデルの問題点を整理して、それを克服するためのアイデアをいくつか考えていたことがわかります。今回は、主として従来モデルの問題点について書いてみます。
2.Y-U model開発の背景と動機
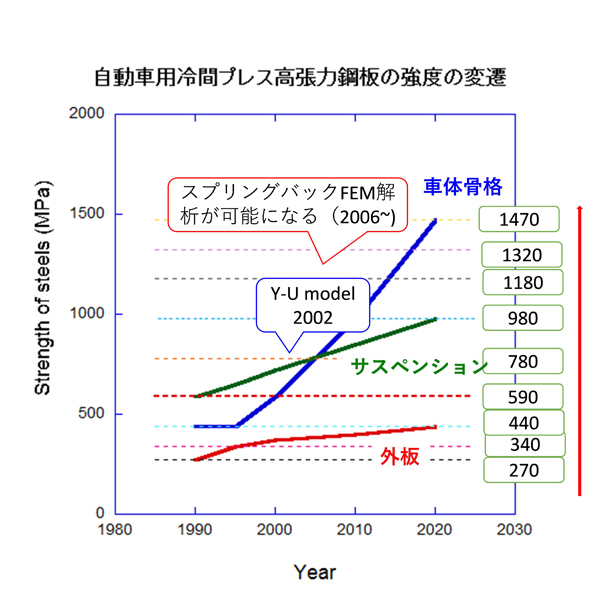
まず2000年頃の板材成形技術の状況についてですが、自動車産業で急速に高張力鋼板が使われだしました(Fig. 1参照)。当時は590MPa鋼板が主でしたが、それでもスプリングバック予測とその克服は大きな技術課題でした。一方、板材成形シミュレーションは産業界でかなり使われてきていましたが、スプリングバックの計算は全くできない、ひどい時にはスプリングバックの方向さえ実際とは反対に予測することがあるような状況でした。これは、世界中の板材成形シミュレーションソフト開発(リリース)会社にとっても乗り越えなければならない大きな壁でした。
ここで議論の理解を深めるために、スプリングバックの力学基礎について簡単に説明します。スプリングバックは、Fig. 2に示すように、板が曲げられた時の曲げモーメント \(M_0\) が駆動力となって、曲げモーメント \(M\) が解放 \((M=M_0\to0)\) されるときの曲げの戻りです(曲率変化 \(\Delta\kappa\) 。これは主に弾性変形ですが、後述のようにバウシンガー効果のために弾塑性変形になることもあります)。簡単のために、スプリングバックが弾性変形だとすると、スプリングバック \((\Delta\theta\mid\theta=\Delta\kappa\mid\kappa)\) は板のヤング率 \(E\) とパネルの形状剛性 \(I\) を用いて次式のように表されます。
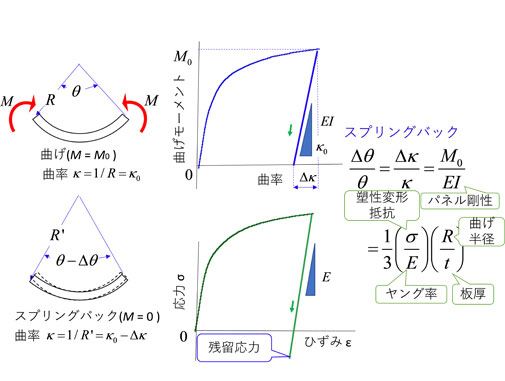
\[\frac{\Delta\theta}{\theta}=\frac{\Delta\kappa}{\kappa}=\frac{M_0}{EI}\]
すなわち、スプリングバックの正確な計算のためには、駆動力である曲げモーメント \(M_0\) が高精度に計算されることと、スプリングバック時の材料の実際のヤング率の値を用いることが不可欠です。曲げモーメント \(M_0\) は、成形の最終段階で板に発生している応力から計算されますので、応力計算の精度がスプリングバックの計算精度に直接関係します。また、後述するように、塑性変形を受けた材料のヤング率 \(E\) (除荷時の応力-ひずみ勾配)は一定値ではなく、塑性ひずみが大きいほど小さな値となります。材料のバウシンガー効果のため、スプリングバックのときに再降伏することもあります。このように、スプリングバック過程での材料特性はスプリングバックの計算精度を大きく左右します。
ということで、私は、スプリングバック計算の精度が悪いのはシミュレーションに使っている材料モデルに大きな原因のひとつがあると思っていました。とくにバウシンガー効果を無視している(すなわち当時の全てのシミュレーションソフトが等方硬化モデルを使っている)ことが大きな問題との認識でした。とりわけ、ドローベンドのように板材が繰り返し曲げ・曲げ戻しを受けるようなケースのシミュレーションではバウシンガー効果の考慮は不可欠です。そこで、2000年前後の国際会議等ではそのことを機会があるたびに主張していました。しかし、それに対する他の研究者の反応はあまり芳しいものではなく、移動硬化モデルに対する認識もPrager-Zieglerの古典的線形移動硬化をイメージする研究者が多いような状況でした。そこで私は、成形シミュレーション・スプリングバック解析に使える大ひずみ繰返し塑性モデルを自分で提案しようと決めました。というのは、それまでの非線形移動硬化モデルは、原子力・重工分野などの疲労問題への応用がほとんどで、塑性ひずみがせいぜい1~2%程度を想定したものだったからです。私自身もそのような分野で長く研究をしていたため、大ひずみ繰返し塑性モデルの重要性は十分に認識できました。
3.大ひずみ繰返し塑性モデルのポイント
少し以前のエッセイの繰返しになりますが、大ひずみ域で板材成形シミュレーションの高精度化と大きく関係する弾塑性挙動は次のようになります。
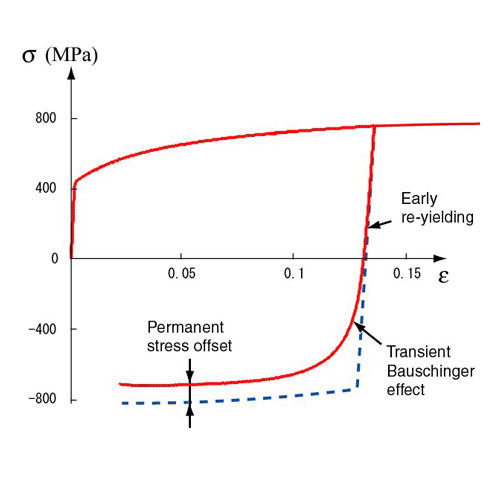
- (1) 応力反転後の再降伏は極めて早い段階で起こり、その後、加工硬化率が急激に変化する遷移的バウシンガー効果、永久軟化(バウシンガー効果がないと仮定した場合より流動応力が小さい)が起こる(Fig. 3参照)。
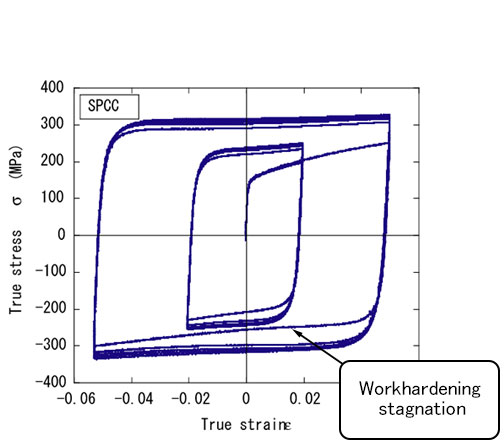
- (2) 繰返し加工硬化は数回のひずみサイクルでほぼ収束するが(注:硬化収束までのサイクル数は材料に依存する)、大きな繰返しひずみ幅のサイクルほど大きな応力振幅に収束する(Fig. 4参照)。
- (3) 応力反転時(遷移バウシンガー効果直後)に加工硬化が一時休止したような挙動(workhardening stagnation、Fig. 4参照)が見られる。
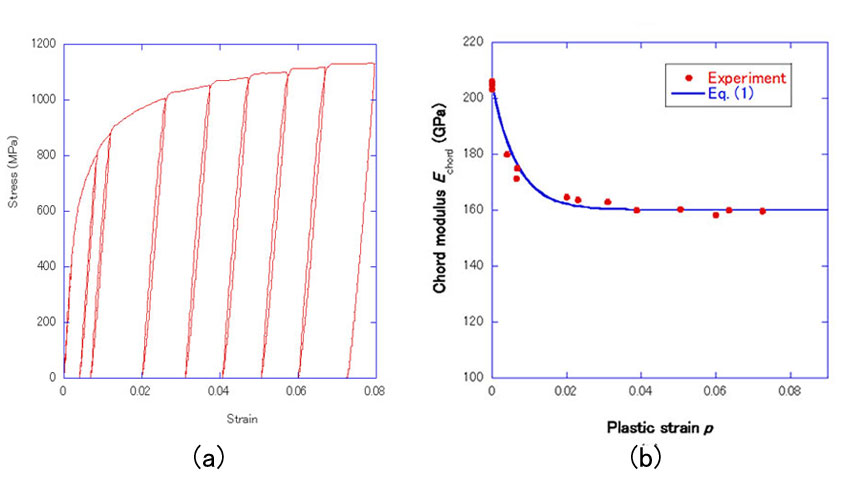
- (4) 引張り塑性変形後の除荷・再負荷試験(Fig. 5(a)参照)における応力-ひずみ応答は教科書に書いてあるような直線ではなく、わずかに曲線となっており、除荷の応力-ひずみの線形近似勾配(便宜的にこれをヤング率と呼ぶ)は塑性ひずみとともに低下する(Fig. 5(b)参照)。この現象を「ヤング率の塑性ひずみ依存性」と呼ぶ。
教科書に書いてあるような直線ではなく、わずかに曲線となっており、除荷の応力-ひずみの線形近似勾配(便宜的にこれをヤング率と呼ぶ)は塑性ひずみとともに低下する(Fig. 5(b)参照)。この現象を「ヤング率の塑性ひずみ依存性」と呼ぶ。
ここで、従来の非線形移動硬化モデルでこれらがどこまで記述できるのかについてみてみましょう。Chaboche model4)の実用バージョンである、式(2)-(4)に示す、等方硬化(IH)+Armstrong-Frederick(A-F)非線形移動硬化(NLK)+線形移動硬化(LK)を使うことにします。
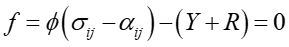
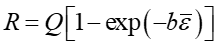
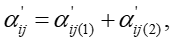
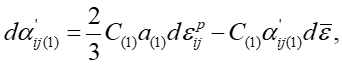
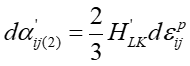
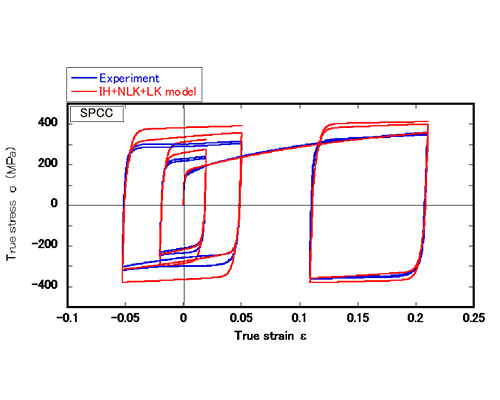
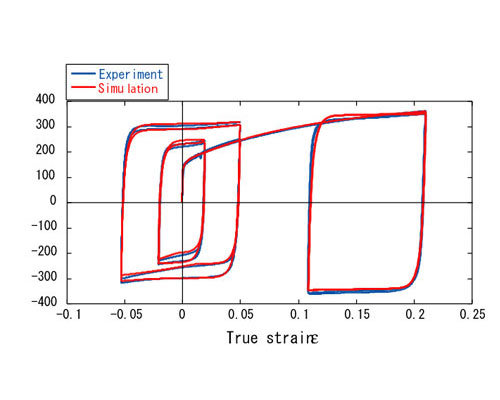
Fig. 6ではSPCC鋼板の繰返し弾塑性応力-ひずみ応答のシミュレーション結果と実験結果の比較を示します。これからわかることは、上記(1)のバウシンガー効果はある程度は表現できているものの、(2)の繰返し硬化については繰返し数が大きくなるにつれて過大に計算されています。これは、式(3)からわかるように、等方硬化応力 \(R\) が相当塑性ひずみ \(\bar{\varepsilon}\) の一義的関数となっているため、繰返し変形で塑性ひずみが累積されるとともに加工硬化がどんどん進んでゆくからです。(3)の「workhardening stagnation」と(4)「ヤング率の塑性ひずみ依存性」についてはIH+NLKH+LKH modelでは全く考慮していません。比較のために、Y-U modelを用いたシミュレーション結果をFig. 7に示します。
4.おわりに
今回は、大ひずみ弾塑性繰返し塑性で表現すべき重要な弾塑性挙動(従来モデルでは表現できなかったもの)について概括的なお話しをしました。次回ではY-U modelではこれらをどのように表現しているのかについて、モデル化にあたって考えたことも含めて、具体的に解説したいと思います。
- Yoshida, F., Uemori, T., Fujiwara, K., 2002. Elastic-plastic behavior of steel sheets under in-plane cyclic tension-compression at large strain. International Journal of Plasticuty 18, pp.633-659.
- Yoshida, F., Uemori, T., 2002. A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation. International Journal of Plasticity 18, pp.661-686.
- Yoshida, F., Uemori, T., 2003. A model of large-strain cyclic plasticity and its application to springback simulation. International. Journal of Mechanical Sciences 45, pp.1687-1702.
- Chaboche, J.L., Rousselier, G., 1983. On the plastic and viscoplastic constitutive equations, part I and II., ASME Journal of Pressure Vessel Technology, 105, pp.153-164.
- ※ 記載されている製品およびサービスの名称は、それぞれの所有者の商標または登録商標です。
技術ブログカテゴリ
新着記事
- 分子シミュレーションで設計するプラスチックリサイクル
- 形状設計フェーズでの組み立て精度向上によるコスト削減
~ 組み立てCE検討ツールのご紹介 ~ - JSOLが考える「溶接シミュレーションと工場デジタルツインが実現する工程設計」について講演しました
- リアルワールドの自動車衝突安全に向けて
- 機械学習で加速する材料シミュレーション技術
- ノウハウ不要!樹脂の複雑な材料特性を簡単にフィッティング 〜 材料同定ツールと高精度ユーザーサブルーチンの活用事例 〜
- 樹脂材やゴム材の高精度予測に向けたパラメータ同定
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(後編)
- データ活用からナレッジ活用へ ~ モードによる評価と履歴データの活用 ~(前編)
- 製造業におけるマテリアルズ・インフォマティクス
