8．Yoshida-Uemori model（その２）
- 塑性力学、材料モデルの研究に魅せられて -

1．はじめに

まずはじめに、本エッセーを長い間中断していたことを深くおわび申し上げます。今回からは、Yoshida-Uemori (Y-U) model^1)-3)の具体的な内容についてお話しをさせていただきます。先回から大分時間が経ってしまいましたので、話の筋を理解しやすくするために、先回までの重要なポイントを繰返している部分もありますが、ご容赦ください。
先回の「Yoshida-Uemori model（その1）」で述べた、板材成形シミュレーションの高精度化と大きく関係する弾塑性挙動は次のようになります。

• （1）応力反転後の再降伏は極めて早い段階で起こり、その後、加工硬化率が急激に変化する遷移的バウシンガー効果、永久軟化が起こる。
• （2）繰返し加工硬化について，、大きな繰返しひずみ幅のサイクルほど大きな応力振幅に収束する。
• （3）応力反転時（遷移バウシンガー効果直後）に加工硬化が一時休止したような挙動（workhardening stagnation）が見られる。
• （4）引張り塑性変形後の除荷・再負荷試験における応力−ひずみ曲線の線形近似勾配（便宜的にこれをヤング率と呼ぶ）は塑性ひずみとともに低下する。

私は、材料モデルを考えるに当たり、ほぼ全ての金属材料に共通のこれらの弾塑性挙動（1）〜（4）を表現できるものを作ろうと思いました。以下では、それがどのようにY-U modelで記述されているのかを解説します。

2．Y-U modelの枠組み：二曲面モデル

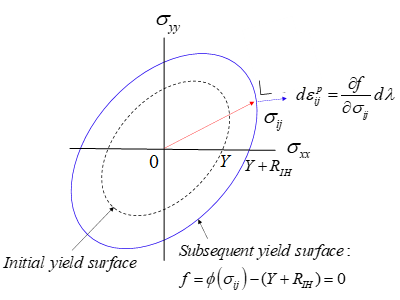
材料の加工硬化を表現する最も簡単なモデルは、降伏曲面が拡大する（Fig. 1参照、降伏曲面の大きさ \(Y \to Y + R_{ IH }(\bar{\varepsilon})\)) とする等方硬化モデル(isotropic hardening [IH] model)です。これは、初期降伏曲面を降伏関数 \(\phi(\sigma_{ ij } )\) 、初期降伏応力 \(Y\)を用いて以下のように表すと

• 画像拡大

  Fig. 1　等方硬化モデル

• 画像拡大

  Fig. 2　移動硬化モデル

• 画像拡大

  Fig. 3　複合硬化モデル

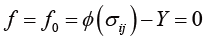
次式で表せます。

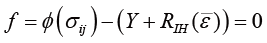
等方硬化応力 \(R_{ IH }(\bar{\varepsilon})\) は相当塑性ひずみ \(\bar{\varepsilon}\) の一義的関数で表されていますので、加工硬化は応力の方向には依存しない、すなわちバウシンガー効果を表現できません。材料のバウシンガー効果を表現する標準的なモデルは、降伏曲面の中心（＝backstress： Fig. 2の \(\alpha_{ ij } \) )が塑性変形とともに移動する移動硬化モデル(kinematic hardening [KH] model)です。これは次式で表せます。

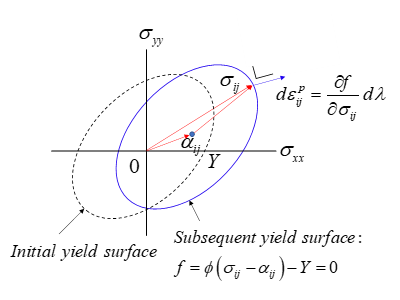
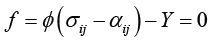
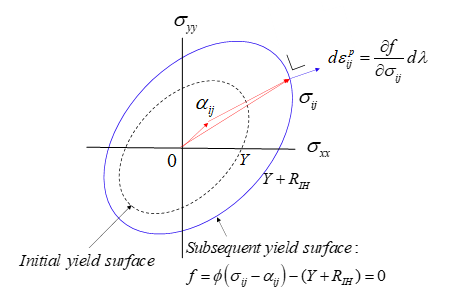
この二つのモデル（等方硬化と移動硬化）を組み合わせて、降伏曲面が塑性変形とともに拡大しながら中心も移動することを仮定する複合硬化モデル（IH+KH combined hardening model，Fig. 3参照）が最も普通の塑性モデルです。これは次のように書けます。

• 画像拡大

  Fig. 4　Y-U二曲面モデル

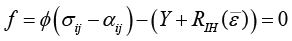
しかし、Y-U modelの枠組みは、上述した通常の複合硬化モデルとは違っています。Y-U modelでは、降伏曲面は塑性変形によって拡大せず、移動だけを仮定します。その意味では完全な移動硬化モデルです。それでは、材料の加工硬化をどのように表現するかというと、降伏曲面が移動する範囲（これを境界曲面：bounding surface Fで表します。Fig. 4参照）が塑性変形とともに拡大することにより表現します。すなわち、降伏曲面の移動則を境界曲面の拡大（＋わずかな移動）と関連付けて以下のように表現します。

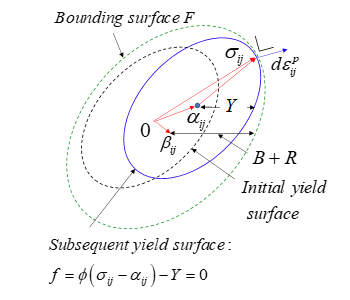
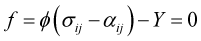
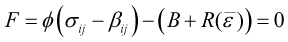
ここで、 \(B\) は境界曲面の初期（未変形状態）の大きさ、 \(R(\bar{\varepsilon})\) は境界曲面が塑性変形とともに拡大（等方硬化）する量を示しています。なお、このモデルでは応力反転における永久軟化を表すために、境界曲面のわずかな移動 \((\beta_{ ij } )\) も仮定しています。

• 画像拡大

  Fig. 5　DP980鋼板の応力反転時の応力―ひずみ挙動の実験結果と複合硬化モデル（Armstrong-Frederick移動硬化+等方硬化[AF-KH+IH]）およびY-Uモデルでのシミュレーション結果の比較

では、なぜ降伏曲面の拡大ではなく、降伏曲面の移動する範囲を拡大するモデルにしたかというと、実験結果から見て、応力反転後の再降伏は極めて早期に起こっていて、降伏曲面（弾性範囲）が塑性変形に伴って拡大しているとはどうしても思えなかったからです。一例として、Fig. 5では、DP980鋼板の応力反転時の応力―ひずみ挙動の実験結果と複合硬化モデル（Armstrong-Frederick^4）移動硬化+等方硬化[AF-KH+IH]）およびY-U modelでのシミュレーション結果を比較しています。これを見てもわかるように、応力反転時の再降伏点（re-yielding）はY-U modelのほうが明らかに現実的であることがわかります。

3．おわりに

今回は、Y-Uモデルの二曲面モデルの枠組みについて説明しました。次回は、Y-Uモデルにおける移動硬化則（backstress \(\alpha_{ ij } \) がどのように塑性変形とともに変化するか）について解説します。