ライフサイエンス／バイオマテリアル分野のための分子シミュレーション

ライフサイエンス／バイオマテリアル分野の製品は、医薬品、食品、化粧品、バイオプラスチックなど多岐にわたります。これらはタンパク質、薬物候補化合物、生体適合ポリマー、脂質、糖類、核酸など、さまざまな生体関連分子から作られています。そのため、設計における各機能の予測、最適化にあたっては、分子の構造や運動性、分子間の親和性などの理解が重要となります。本記事では、これらの機能最適化のための分子シミュレーションの活用例をご紹介します。

分子レベルの現象と製品機能との関係

前述のように、生体関連製品の機能は、分子レベルの運動性、親和性が密接に関係しています。たとえば創薬においては、タンパク質が薬物候補化合物(リガンド)と結合することで機能を制御します。バイオマテリアルの設計でも、バイオセンサーや生体適合性素材において、タンパク質と樹脂との親和性が重要な要素となります。機能性食品ではペプチドが酵素タンパク質に影響を与え、体内での種々の物質の分解を制御するほか、食感の部分でも多糖類と溶媒から生じる粘性や、分子構造が作るネットワーク構造が大きく影響します。また、製剤設計では担体（キャリア）となるポリマーや脂質等と、原薬の作る相構造が可溶化能や標的への送達性能を決定します。洗剤や化粧品等の化成品においても、界面活性剤の親和性が性能に直結します。これらの機能を理解し、設計するために、原子単位のミクロな運動・結合親和性や分子集団の相分離など、複数のスケール（マルチスケール）での現象を考慮したさまざまなシミュレーション技術が活用されています。

さまざまな現象に対応する分子シミュレーション

分子動力学(MD)法は分子を球とばねで表現し、ニュートンの運動方程式を解くことで、構造や運動性、親和性を計算する手法です。原子ごとに1つの球で表現した全原子MDでは、原子レベルの微細な運動をシミュレーションすることができます。たとえば、受容体とリガンドの親和性解析や、官能基の微細な違いによる結合様式の差異など、ナノメートルサイズでの精密な計算に利用されています。また、分子ドッキング計算（受容体分子にリガンドを嵌めこみ、さまざまな安定構造を探索する手法）とMDを組み合わせた、インシリコスクリーニングと呼ばれるリガンドの順位付けが一般的に実施されています。親和性評価にはMM-GB/SA[1]や自由エネルギー摂動法[2]など、目的に応じて精度や計算コストの異なる手法が確立されています。全原子MDでは原子種ごとに適切な相互作用、骨格パラメータを割り当てる必要があり、生体分子ではAMBERやCHARMM, OPLSといった力場パラメータが広く使用されています。力場についての詳細は [分子動力学で使われる力場の発展]をご覧ください。

粗視化シミュレーションは任意の原子団を1つの球とすることで、全原子MDと比べて大規模、長時間のシミュレーションを可能にする技術です。複数原子を1つの球で表現するため、細かな描像は失われてしまいますが、各官能基や部位が持つ性質を保ったまま、分子の変形・凝集を計算することが可能です。近年の生体分子においては、Martini力場[3,4]と呼ばれる汎用力場による粗視化シミュレーションが広く活用されています。全原子MDとくらべ約100倍の速度で計算することが可能で、タンパク質等は全原子構造をそのまま粗視化構造に変換して解析する技術が整備されています。図1に、Martini力場の原子構造との対応関係の図[5]と、ミトコンドリアタンパク質超複合体の計算例[6]を示します。

相分離計算にはより高速な散逸粒子動力学(DPD)[7]を用います。摩擦や熱揺動など、流体の効果が含まれており、数10〜100nmのサイズを用い、全原子MDの1000倍以上の速度で計算することが可能です。図2の左に示すような相分離構造を短時間で予測することができます。散逸粒子動力学では粒子間の親和性に高分子の親和性を示すχパラメータ[8]を用いることが一般的です。原子構造からχパラメータを推算するさまざまな方法と組み合わせて実際の対象に適用されます。

また、原子よりも細かな電子単位に注目した、量子化学計算による高度な親和性解析も有効に実施されています。フラグメント分子軌道法(FMO)[9]は、分子をフラグメントに分割した全電子計算で、フラグメント間相互作用の成分分解（PIEDA）により、相互作用の要因を解析できるのが大きな特徴です。図2の右に示すように、相互作用を静電力、分散力、電荷移動由来などに分解し、部位が持つ相互作用を解析することができます。対象によっては分子動力学と組み合わせ、一部だけを量子化学で扱うQM/MM法[10]を活用することにより、結合ポケットの反応解析なども扱うことができます。

図1. Martini粗視化モデル(左、文献[5]より転載。CC BY Attribution 3.0 Unported ライセンスの下で使用)と、ミトコンドリアタンパク質超複合体の計算
(右、文献[6]より転載。CC BY Attribution 4.0 International ライセンスの下で使用)

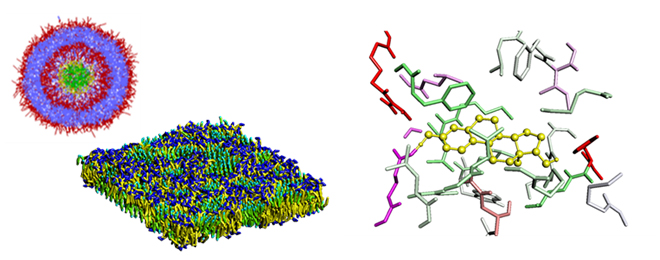図2. DPDによる生体膜の相分離計算とFMOによる創薬ポケットの親和性計算

特に創薬研究において、タンパク質と薬物候補化合物の親和性の評価には、適切な結合構造の準備が不可欠です。しかし、精密な立体構造が実験で必ずしも得られるとは限りません。そのため、シミュレーションによる結合ポーズ推定が行われますが、単純な全原子MDでは、初期配置から構造が大きく動かず、適切な安定配置までたどりつけないケースが多く発生します。そこで拡張アンサンブルと呼ばれる手法により、複数の条件のMDを組み合わせることで、適切な安定配置を探索します。たとえば理化学研究所を中心に開発されているGENESIS[11,12]のgREST [13]は、系の一部の温度のみを上昇させ、効率的なサンプリングが可能な手法です。ドッキング計算を用いて簡易的にタンパク質に化合物分子を嵌めた構造を用意し、ポケット付近のみの構造サンプリングを行うことで、適切な安定構造が得られる事例が報告されています[14]。また図3に示すように、COVID-19のスパイクタンパク質のような大きなタンパク質に適用することにより、新たな創薬候補ポケットの探索にも活用も模索されています[15]。近年の多様な創薬モダリティに対応するため、さまざまな構造を解析するためのサンプリング技術がますます重要になると考えられます。

図3. gREST法によるCOVID-19新規創薬ポケットの探索
（文献[15]より転載。CC BY Attribution 4.0 International ライセンスの下で使用)

製剤、化成品分野での粗視化シミュレーション活用

薬物における送達性能の制御は、ドラッグデリバリーシステム（DDS）とよばれます。分子製剤学の分野では最近、DPDシミュレーションを用いて、ミセル、ナノ粒子、膜形成に関する自己組織化の研究が多数実施されています[16]。COVID-19ワクチンなどにおいて脂質ナノ粒子(LNP)やリポソームといった脂質粒子がキャリアとして使用された関係で広く認知されるようになり、図4右に示すように、Martini粗視化モデルでも脂質を対象に多くの研究がなされています[17]。また図4左のように、非晶質固体分散体など、近年多くを占めている難溶性薬物の可溶化技術の研究にも適用されており、ユニットごとに粗視化した担体とポリマーの相分離シミュレーションや、pHによる分散構造の違いを検討した例などが報告されています[18]。
化粧品や洗剤等の化成品の分野でも自己組織化は重要なテーマです。近年注目されている生体由来の各種界面活性剤の親和性や、自己組織化もシミュレーションを用いて議論されています[19]。

図4. DPDによる固体分散体のシミュレーション（左、文献[18]より転載）と、
MartiniのLNPシミュレーション（右、文献[17]より転載）
いずれもCC BY Attribution 4.0 International ライセンスの下で使用。

バイオマテリアル分野でのシミュレーション活用

バイオマテリアル分野においては、過去に材料シミュレーションで蓄積されてきた技術を活用することができます。たとえばカーボンニュートラル材料として注目を集めているセルロースナノファイバー(CNF)は電場による制御が行われますが、図5左に示すように、分子動力学を用いることで任意の電場をかけた際の配向を解析することができます[20]。また、バイオマスプラスチック、フィルムにおいて重要な機能の1つである複屈折は、伸張計算により解析することが可能です。バイオ由来でない材料の事例ですが（粗視化分子動力学を用いた複屈折の解析）粗視化MDの活用が有効な手段として挙げられます 。バイオマスプラスチックにおいても、同じような解析が実施可能です。その他、図5右に示すように、グラフェンセンサーによる核酸の認識についても全原子MDの範囲で解析が実施されているほか[21]、食品の着色にも分子間相互作用が大きく関わっており、キタンサンガムと黒米のアントシアニンの色安定性に及ぼす影響と作用機序などもＭＤにより解析されています[22]。

図5. CNFへの電場印加(左)[20]や、グラフェンシートと核酸の相互作用解析（右）[21]CNFへの電場印加(左、文献[20]より転載）と、グラフェンシートと核酸の相互作用解析（右、文献[21]より転載)
いずれもCC BY Attribution 4.0 International ライセンスの下で使用。

J-OCTAではGENESIS[11,12]による高度なMDや、Martini[3,4]による粗視化MD、COGNAC[23]によるDPDシミュレーション、ABINIT-MP[24]によるFMO解析が実施可能です。
これらのシミュレーションにご興味がございましたら、ぜひお気軽にこちらまでお問い合わせください。