
CAE Technical Library エンジニアレポート - CAE技術情報ライブラリ
分子動力学(Molecular Dynamics、以下MD)計算は今日では広く使われるシミュレーション手法です。今回は MD計算で使われる力場(Force field)について、その分類と最近の発展を概観します。
力場とは MD計算に必要な力やエネルギーを経験的な式で表せるようにしたもので、この式に含まれるパラメータを力場と言います。力場は 1970年代から種々のものが開発されています。本記事では主に有機系をターゲットとした力場の分類を紹介するとともに、最近の発展として反応性力場や機械学習の活用まで触れたいと思います。
分子動力学計算と原子に働く力
まず MD計算で行われている計算の中身について、簡単に確認しておきましょう。MD計算では、ある時刻における粒子に働く力を計算し、その運動をニュートン方程式に基づいて解きます。これを逐次的に繰り返し、長時間の運動について解析することができます。粒子位置 x の時間変化はテイラー展開により以下のように表せます。
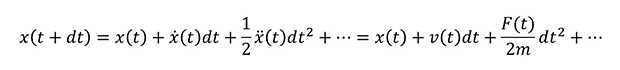
ここで.(ドット)の付いた x は位置 x の時間による一階微分、..(ツードット)が付いた x は二階微分であり、それぞれ速度vと力Fに対応します。実際の MD計算では Verlet の方法などが使用され、導出は省きますが時間積分は以下のようになります。
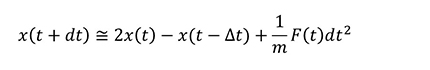
つまり、MD計算には力Fが必要であるということが分かります。
力やエネルギーは第一原理計算手法(密度汎関数理論、DFTなど)を使えば計算することができ、実際にそのような手法も使われています。これは、第一原理MD計算(AIMD、Ab initio MD)と呼ばれ、力場パラメータが存在しない系でMD計算を行う場合には有用な方法となります。
ただし、非常に高コストな計算になるため、従来のMD計算では、力は経験的な式により計算されていました。
分子動力学計算で使用される力場の種類
古典力場ではクラス I、II、III といった分類がされています。
クラスI力場は以下のようにポテンシャルエネルギーU はボンド、アングル、トーションとLJ相互作用、静電相互(ES)作用から成ります。このような力場の代表例として DREIDING、AMBER、GAFF、OPLS などがあります。
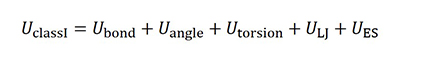
クラスII力場ではクラスIのポテンシャルエネルギーに追加してボンド‐ボンドやボンド-アングルのカップリング項が含まれます。このような力場としてはPCFFなどがあります。

クラスIII力場はさらに電荷の分極効果(電荷分布が時間的にゆらぐ効果)を取り入れたものなどが提案されています。(クラスI、II では、電荷は基本的に原子上に固定された点電荷になっています。)
これらの力場では汎用的に分子を扱うことができますが、特別にチューニングされたモデルが提案されている分子もあります。たとえば水の場合はチューニングされたモデルが多く提案されており、代表的なものとしては SPC、SPC/E、SPC-FW、TIP3P、TIP4P、OPC3 などが知られています。
水分子は3原子からなりますが、水モデルの相互作用点は3点のものと、4点以上持つものがあり、TIP4P は4点モデルです。また SPC-FW を除く多くのモデルで水分子は剛体として扱われるため、適切な拘束条件(SHAKE法、RATTLE法)の下で MD計算が行われます。
※ J-OCTA の COGNACモデラでは TIP3P、SPC-FW のパラメータを設定して用いることができます。
GENESISモデラでは SPC/E、TIP3P、OPC3モデルを使用することができます。
これらのモデルでは計算される物性値に差があります。
詳細は以下ページを参照してください。
https://water.lsbu.ac.uk/water/water_models.html
このような形式の力場はおもに有機分子を対象に使われており、無機物の場合には異なるタイプの力場(EAMやTersoff)が使用されています。また有機-無機界面などでは、適当な力場パラメータがないことがあり、密度汎関数理論(Density Functional Theory、以下DFT)計算に基づいて非結合相互作用パラメータを決めるDFT-MD連携の試みなどがあります。[1]
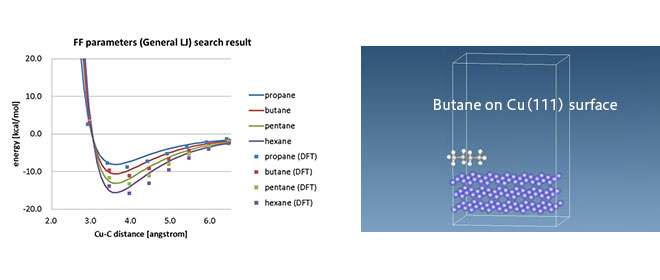
※ J-OCTA では DFTソフトとして SIESTA を用いたLJパラメータ決定機能を提供しており、有機無機界面の MD計算を実施できます。 [J-OCTA解析事例] 金属表面と分子の相互作用
以上で説明した力場は基本的に分子の安定状態を扱うものですが、2000年代以降、反応過程も含む計算が可能な反応性力場(代表的なものとして ReaxFF[2])が提案されています。
反応を含む MD計算は大きく分けて2つあり、反応過程を詳細に追跡したい場合と、反応を経た後の構造に興味がある場合です。ReaxFF は前者の反応過程を詳細に追跡する目的で用いられます。
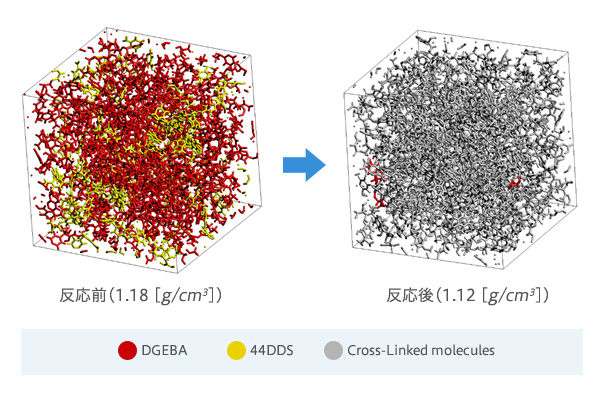
※ J-OCTA/VSOPは熱硬化性樹脂(反応を経た後の構造に興味がある場合)での実施例があります。
[J-OCTA解析事例] 活性化エネルギーを用いたモンテカルロ判定によるエポキシ樹脂の架橋反応
さらに最近では機械学習を用いた力場(ML力場)が提案されています。
ML力場は、AIMD に近いレベルの精度が得られるという反面、計算コストは古典力場よりも大きくなります。主に無機物への適用が先行していますが、有機系への適用もあり、今後の発展が期待されています。[3-5]
今回ご紹介した力場の種類と概略を表1 にまとめました。
2023年において、HPC環境やクラスターマシンを利用した古典力場による MD は、100ナノ秒以上の計算がスタンダードになりつつあります。ML力場は計算コストが古典力場よりも大きくなるため、古典MDほどの長時間計算が難しいことから適用課題は慎重に選択する必要があります。表1 に記載した計算速度は概算です。AIMD とそれ以外ではスケーリングが異なりますが、検討の際の目安のひとつになれば幸いです。[6]
表1. MD計算で使用される力場の種類
| 力場の種類 | エネルギーへの寄与 | 力場セット | 計算速度 |
|---|---|---|---|
| クラスI | 結合性、非結合性 | AMBER、GAFF、OPLSほか | 1 |
| クラスII | クラスIに結合性カップリング項 | UFF、PCFFほか | : |
| クラスIII | クラス I/IIに分極効果など | AMOEBAほか | : |
| 反応力場 | 文献[2]を参照 | ReaxFFほか | : |
| ML力場 | 文献[3-5]を参照 | DeepMDほか | 0.01 |
| 第一原理 | DFTなどに基づく | 力場は不要 | < 0.0001 |
- 参考文献
-
- [1] K. Johnston and V. Harmandaris, J. Phys. Chem. C, 115 14707 (2011)
- [2] A.C.T. van Duin, et al., J. Phys. Chem. A, 105, 9396 (2001)
- [3] V. L. Deringer, et al., Chem. Rev., 121, 10073 (2021)
- [4] E. Kocer, T. W. Ko and J. Behler, Annu. Rev. Phys. Chem., 73, 163 (2022)
- [5] T. Wen et al., Mater. Futures, 1, 022601 (2022)
- [6] L. Zhang, et al., Phys Rev. Lett., 120, 143001 (2018)





