機械学習で加速する材料シミュレーション技術

近年、機械学習（ML）技術は材料科学における革新的アプローチとして注目されており、材料シミュレーション技術との融合が進んでいます。たとえば、構造物性相関（Quantitative Structure-Property Relationship, QSPR）のための機械学習モデルは、分子構造から物性値を予測する手法として広く用いられています。本記事では、最近のトピックとして機械学習ポテンシャルや生成モデルなどを取り上げ、これらと材料シミュレーション技術との連携によってシミュレーションの適用範囲が拡大している状況について紹介したいと思います。

QSPRによる物性予測

はじめに、QSPRのための機械学習の利用について簡単にご紹介します。機械学習により、分子のフィンガープリントや量子化学計算に基づく記述子（例：HOMO-LUMOギャップ、極性表面積、分子体積など）を特徴量として抽出し、融点^[1]、沸点^[2]、ガラス転移温度^[1]、粘度^[3]などのマクロな物性を予測する回帰モデルが構築されます。これらのモデルは、第一原理計算や分子動力学法の代替手段（サロゲート）として機能し、計算コストの大幅な削減を可能にします。
使用されるアルゴリズムには、ディープニューラルネットワーク（DNN）やランダムフォレストに加え、分子構造をグラフとして扱うGraph Convolutional Network（GCN）などのグラフベースの深層学習モデルが含まれます。これらの技術により、材料探索の高速化が実現され、マテリアルズ・インフォマティクス（Materials Informatics）によるデータ駆動型の材料設計が急速に進展しています。

機械学習ポテンシャル（MLIP）とその代表的モデル

近年、材料科学の分野で注目を集めている技術のひとつがMLIP（Machine Learning Interatomic Potential）、すなわち機械学習ポテンシャルです。MLIPとは、第一原理計算、特に密度汎関数理論（DFT）と同等の精度でポテンシャルエネルギー面（PES）を再現しながら、計算コストを大幅に削減できる手法を指します。初期の代表例としてはBehler-Parrinello型ニューラルネットワーク^[4]やGaussian Approximation Potential（GAP）^[5]、DeepMD^[6]、aenet^[7]などがあり、近年ではNequIP^[8]やMACE^[9]などの汎用性の高いモデルも登場しています。図1はNequIPによる計算結果を示しており、ここからAIMDと非常に近い精度であることが分かります。これらのモデルの学習には、高精度なエネルギー・力・応力テンソルを含むデータセットが不可欠であり、代表的なものとしてMD17（小分子のDFTに基づく動力学データ）^[10]、ANI-1x（有機分子の広範な構造空間をカバーしたデータ）^[11]、Materials Project（無機物質を広くカバーしたデータ）^[12]やOpen Catalyst Project（無機材料の触媒反応系のデータ）^[13]などが活用されています。最近Meta社から一億以上のデータを含むOMol25データセット^[14]が発表され、この分野の注目度が高いことが分かります。CHGNet^[15]やMACEでは学習済みの汎用ポテンシャルが公開されており、ユーザ側で学習を行わずともMLIPを使えるようになりました。ただし、MLIPは反応経路探索や欠陥構造解析、触媒設計などにおいて強力なツールとなる一方、古典力場を用いたMDよりも計算コストが高いため、長時間スケールの緩和現象などには不向きです。適切な応用範囲を見極めた上で、DFTとのハイブリッドな活用が求められます。

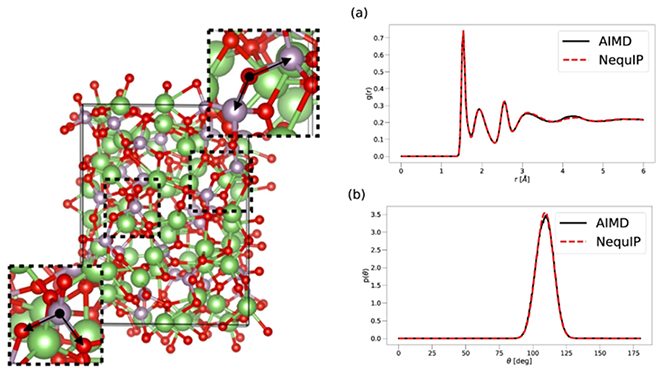図1. MILP（NequIP）を使用した計算結果の第一原理計算（AIMD）との比較
Li4P2O7（左）の RDF（a）、Pを中心とする角度分布（b）。文献[8]より転載。
CC Attribution 4.0 International Licenseのもとで一部改変して使用。

生成モデルの応用とマルチスケールシミュレーション

敵対的生成ネットワーク（GAN）や変分オートエンコーダ（VAE）といった生成モデルは、学習データに基づいて新たなデータを創出する能力を持ち、分子構造の生成や新規分子の設計に広く応用されています^[16]。ここではマルチスケールシミュレーションと関連したトピックをご紹介します。GANなどの技術を粗視化（coarse-grained）モデルから全原子（all-atom）モデルへと復元する「リバースマッピング」に応用する研究も進んでいます。特に、GNN（Graph Neural Network）^[20]やLDB（Latent Diffusion Backmapping）^[21]といった手法は、粗視化されたタンパク質構造から高精度な全原子構造を再構築することを可能にし、構造生物学や分子設計の分野で注目されています。これにより、マルチスケールモデリングの精度と効率が大きく向上しています。
MD-GANはGANをMDと組み合わせたユニークな技術です^[22]。MD計算の短時間のトラジェクトリを学習して生成することができ、この生成を繰り返すことで長時間のトラジェクトリを得ることができます。JSOLでは固体電解質に適用して、固体中のLiイオン拡散について長時間解析を行いました^[23]（図2）。固体電解質は汎用的な古典力場パラメータが用意されていないため、第一原理MDによる解析が必要であり計算コストが問題でした。MD-GANがこの点を効率化することができますし、今後はMLIPとの組み合わせも期待されます。

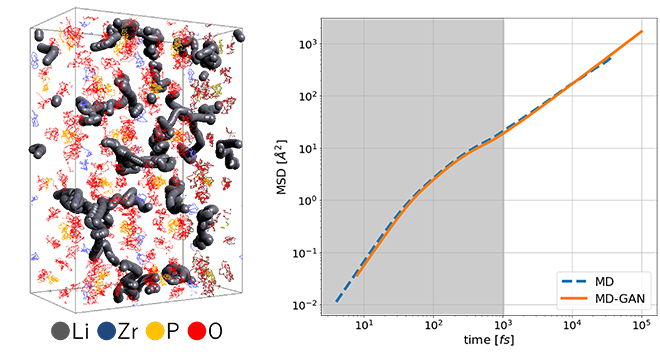図2. MD-GANによる固体電解質中のLiイオンの拡散性の予測

他にもシミュレーションと親和性が高いML技術の応用としては、反応における反応座標（またはCollective Variable）をDNNによって計算する技術^[24]、MDの結果から記述子を抽出する技術^[25]（図3）などがあります。また分子モデリングにおいてML技術を高度に利用する動きも加速しています。AlphaFold^[26]はその代表例で、アミノ酸配列から高精度なタンパク質立体構造を予測可能とし、構造生物学に革新をもたらしました。さらに、大規模言語モデル（LLM）を活用した支援ツールも登場しており、GROMACS Copilot^[27]のように自然言語での入力から分子動力学シミュレーションの設定や解析を自動化する試みが進んでいます。これにより、専門知識を持たずともシミュレーションを手軽に利用できる時代になってきたと言えます。

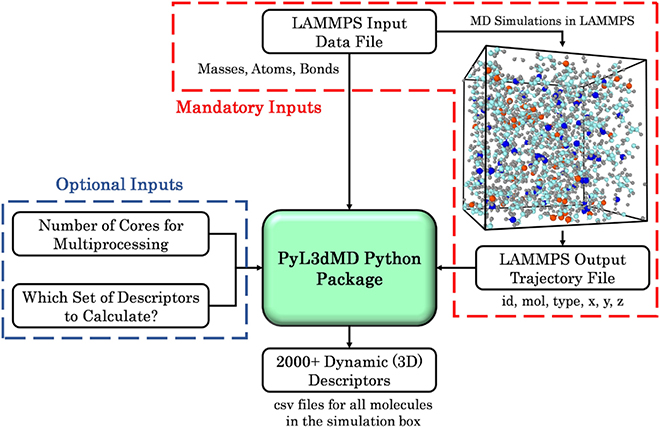図3. MDシミュレーションの結果からディスクリプタを抽出するPyL3dMD.
文献[25]より転載。CC Attribution 4.0 International Licenseのもとで使用。

今後の展望とJSOLの取り組み

このように、機械学習とシミュレーションの連携は、材料科学における多様な課題に対して新たな解決手段を提供しつつあります。QSPRによる物性予測からMLIPによる高精度な力場の構築、さらには生成モデルを活用した構造設計やマルチスケールモデリングの高度化まで、応用範囲は急速に拡大しています。今後は、これらの技術を相補的に活用することで、シミュレーションの効率化と精度向上が一層進展し、材料開発における種々の課題が解決できるようになると期待されます。
JSOLでは、今後も機械学習とシミュレーションの連携のために必要な技術開発や機能開発を続けてまいります。

本記事に記載されていることで、ご相談等がございましたら、遠慮なくご連絡ください。
お問い合わせ