CAE Technical Library 吉田弾塑性工学塾 - CAE技術情報ライブラリ
2019.1.29
2.Bauschinger効果とCyclic Plasticityの研究への入口
塑性力学、材料モデルの研究に魅せられて
株式会社JSOL エンジニアリング事業本部 技術顧問-
画像拡大
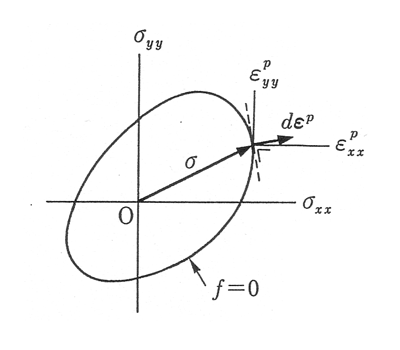
Fig.2-7 塑性ポテンシャル理論
【塑性ポテンシャル理論の基礎】
塑性構成式（応力と塑性ひずみ増分の関係式）の枠組みで最も一般的なのが、「降伏曲面の凸面性」と「塑性ひずみ増分の垂直則」からなる塑性ポテンシャル理論です（関連流動則ともいいます。Fig. 2-7参照）。
（１）降伏曲面 \(f\) は応力
（２）降伏曲面が滑らかな（角点がない）ときは、塑性ひずみ増分ベクトル
したがって、降伏曲面（関数）は、弾塑性判別という本来の意味と同時に、塑性ひずみ増分の進行方向を決定するという重要な役割を持ちます。この理論の詳細については塑性力学の教科書（例えば、吉田[7]）を参照してください。
塑性構成式（応力と塑性ひずみ増分の関係式）の枠組みで最も一般的なのが、「降伏曲面の凸面性」と「塑性ひずみ増分の垂直則」からなる塑性ポテンシャル理論です（関連流動則ともいいます。Fig. 2-7参照）。
（１）降伏曲面 \(f\) は応力
\( \begin{bmatrix} {\sigma}_{ij} \ \end{bmatrix}=\begin{bmatrix} {\sigma}_{xx} & {\tau}_{xy} & {\tau}_{xz} \\ {\tau}_{yx} & {\sigma}_{yy} & {\tau}_{y{z}} \\ {\tau}_{{z}x} & {\tau}_{zy} & {\sigma}_{zz} \ \end{bmatrix} \)
の全ての成分
\( {\sigma}_{ij} \)
をベクトルの独立成分
\({{\sigma}}=\{ {\sigma}_{xx}\ {\sigma}_{yy}\ {\scriptsize \cdots}\ {\tau}_{{z}x} \} \)
とする９次元ベクトル空間（あるいはその部分空間）中で外向きに凸な曲面になる。（２）降伏曲面が滑らかな（角点がない）ときは、塑性ひずみ増分ベクトル
\({d{\varepsilon}}^p=\{{d}{\varepsilon}_{xx}^{\ p}\ {d}{\varepsilon}_{yy}^p\ {\scriptsize \cdots}\ {d}{\varepsilon}_{zx}^{\ p} \} \)
の方向は、降伏曲面
\(f\)
上の応力点において降伏曲面に垂直となる。すなわち式（2）が成り立つ。したがって、降伏曲面（関数）は、弾塑性判別という本来の意味と同時に、塑性ひずみ増分の進行方向を決定するという重要な役割を持ちます。この理論の詳細については塑性力学の教科書（例えば、吉田[7]）を参照してください。
- ■注釈および参考文献■
-
- [1] Yoshida, F., Uemori, T., Fujiwara, K., Elastic-plastic behavior of steel sheets under in-plane cyclic tension-compression at large strain. International Journal of Plasticuty 18, (2002), pp.633-659.
- [2] Yoshida, F., Uemori, T., A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation. International Journal of Plasticity 18, (2002), pp.661-686.
- [3] Yoshida, F., Uemori, T., 2003. A model of large-strain cyclic plasticity and its application to springback simulation. International. Journal of Mechanical Sciences 45, (2003), pp.1687-1702.
- [4] Mroz, Z, On the description of anisotropic workhardening, Journal of the Mechanics and Physics of Solids 15, (967), pp.163-175.
- [5] 吉田総仁、田島直樹、池上晧三、白鳥英亮、メカニカルラチェット現象の塑性力学的検討（異方硬化形塑性ポテンシャルを用いた解析と黄銅材による実験）、日本機械学会論文集43-371(1977)、 pp.2500-2508.
- [6] Shiratori, E., Ikegami, K., Yoshida, F., Analysis of stress-strain relations by use of an anisotropic hardening plastic potential, Journal of the Mechanics and Physics of Solids 27(1079), pp.213-229.
- [7] 吉田総仁、弾塑性力学の基礎、(1997)、共立出版、ISBN4-320-08114-5
※記載されている製品およびサービスの名称は、それぞれの所有者の商標または登録商標です。
